题目内容
若向量
，
满足|
|=|
|=2且
与
夹角为
，则|
+
|= ．
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义，以及性质：向量的平方即为模的平方，即可计算得到．
解答：
解：|
|=|
|=2且
与
夹角为
，
则
•
=2×2×cos
=2．
则|
+
|=
=
=
=2
．
故答案为：2
| a |
| b |
| a |
| b |
| π |
| 3 |
则
| a |
| b |
| π |
| 3 |
则|
| a |
| b |
(
|
|
|
=
| 4+4+2×2 |
| 3 |
故答案为：2
| 3 |
点评：本题考查平面向量的数量积的定义和性质：向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
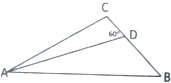爸爸去哪儿节目组安排星娃们露营，村长要求，Feyman、杨阳洋、贝儿依次在A、B、C三处扎篷．AB=8米，BC=4米，AC=6米．现村长给多多一个难题，要求她安扎在B、C两点之间的连线段的D处，且∠ADC=60°．问多多与Feyman相距
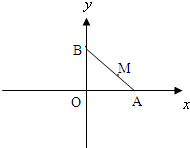如图，线段AB的两个端点A、B分别在x轴，y轴上滑动，|AB|=3，点M是线段AB上一点，且|AM|=1点M随线段AB的滑动而运动．已知函数f（x）=
，若f（2-a）＞f（a），则实数a的取值范围是（ ）
|
| A、（-∞，2） |
| B、（-∞，1） |
| C、（1，2） |
| D、（-∞，-1） |
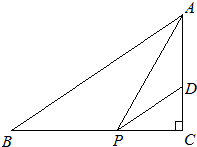如图，直角△ABC中，∠C=90°，AB=2