题目内容
已知椭圆
+
=1(a>b>0)离心率为
.
(1)椭圆的左、右焦点分别为F1,F2,A是椭圆上的一点,且点A到此两焦点的距离之和为4,求椭圆的方程;
(2)求b为何值时,过圆x2+y2=t2上一点M(2,
)处的切线交椭圆于Q1、Q2两点,且OQ1⊥OQ2.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)椭圆的左、右焦点分别为F1,F2,A是椭圆上的一点,且点A到此两焦点的距离之和为4,求椭圆的方程;
(2)求b为何值时,过圆x2+y2=t2上一点M(2,
| 2 |
考点:椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆的方程.
(2)过圆x2+y2=t2上一点M(2,
)处切线方程为2x+
y-6=0,令Q1(x1,y1),Q2(x2,y2),则
,化为5x2-24x+36-2b2=0,由此利用根的判别式、韦达定理,结合已知条件能求出b的值.
|
(2)过圆x2+y2=t2上一点M(2,
| 2 |
| 2 |
|
解答:
解:(1)∵椭圆
+
=1(a>b>0)离心率为
,
椭圆上的一点A到两焦点的距离之和为4,
∴
,
解得a=2,b=
,
∴椭圆的方程为
+
=1.
(2)过圆x2+y2=t2上一点M(2,
)处切线方程为2x+
y-6=0,
令Q1(x1,y1),Q2(x2,y2),
则
,
化为5x2-24x+36-2b2=0,
由△>0,得b>
,
x1+x2=
,x1x2=
,
y1y2=2x1x2-6(x1+x2)+18=
,
由OQ1⊥OQ2,知x1x2+y1y2=0,
解得b2=9,
即b=±3,∵b>
,
∴b=3.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
椭圆上的一点A到两焦点的距离之和为4,
∴
|
解得a=2,b=
| 2 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)过圆x2+y2=t2上一点M(2,
| 2 |
| 2 |
令Q1(x1,y1),Q2(x2,y2),
则
|
化为5x2-24x+36-2b2=0,
由△>0,得b>
3
| ||
| 5 |
x1+x2=
| 24 |
| 5 |
| 36-2b2 |
| 5 |
y1y2=2x1x2-6(x1+x2)+18=
| 18-4b2 |
| 5 |
由OQ1⊥OQ2,知x1x2+y1y2=0,
解得b2=9,
即b=±3,∵b>
3
| ||
| 5 |
∴b=3.
点评:本题考查椭圆方程的求法,考查满足条件的实数值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
,若f(2-a)>f(a),则实数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,1) |
| C、(1,2) |
| D、(-∞,-1) |
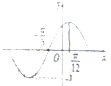 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(4x-
|
算法程序如图所示,若输入-2,执行该程序后输出的y为( )


| A、3 | B、8 | C、16 | D、0 |
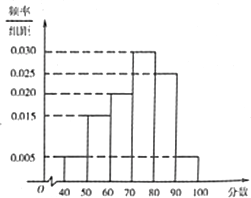 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为