题目内容
下列命题错误的是( )
| A、在△ABC中,“A>B”是“sinA>sinB”的充要条件 | ||||||||||||
B、点(
| ||||||||||||
C、若|
| ||||||||||||
| D、“sinα=sinβ”的充要条件是“α+β=(2k+1)π或α-β=2kπ(k∈Z)” |
考点:平面向量数量积的运算
专题:阅读型,三角函数的图像与性质,平面向量及应用
分析:运用解三角形的知识,正弦定理和边角关系,以及充分必要条件的定义,即可判断A;
由正切函数的对称中心,解方程,即可判断B;
运用向量的数量积和投影概念,即可判断C;
运用诱导公式,即可判断D.
由正切函数的对称中心,解方程,即可判断B;
运用向量的数量积和投影概念,即可判断C;
运用诱导公式,即可判断D.
解答:
解:对于A.A>B?a>b?2RsinA>2RsinB?sinA>sinB,由充分必要条件的定义,可得A正确;
对于B.由y=tanx的对称中心可得,2x+
=
,即x=
-
,k∈Z,令k=1,即为(
,0),
则有B正确;
对于C.由于|
|=1,|
|=2,向量
与向量
的夹角为120°,则
•
=1×2×(-
)=-1.则
在向量
上的投影为2×(-
)=-1,则C错;
对于D.sinα=sinβ?α+β=(2k+1)π或α-β=2kπ(k∈Z),则由充分必要条件的定义,可得D正确.
故选C.
对于B.由y=tanx的对称中心可得,2x+
| π |
| 4 |
| kπ |
| 2 |
| kπ |
| 4 |
| π |
| 8 |
| π |
| 8 |
则有B正确;
对于C.由于|
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
对于D.sinα=sinβ?α+β=(2k+1)π或α-β=2kπ(k∈Z),则由充分必要条件的定义,可得D正确.
故选C.
点评:本题考查解三角形和正弦函数、正切函数的性质,考查向量的数量积和投影的概念,属于基础题和易错题.

练习册系列答案
相关题目
已知函数f(x)=
,若f(2-a)>f(a),则实数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,1) |
| C、(1,2) |
| D、(-∞,-1) |
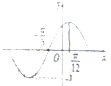 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(4x-
|

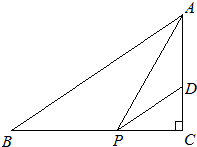 如图,直角△ABC中,∠C=90°,AB=2
如图,直角△ABC中,∠C=90°,AB=2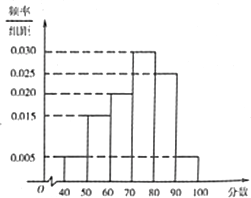 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为