题目内容
P是椭圆
+
=1上任一点,F1,F2为左右焦点
(1)求椭圆的顶点坐标,长轴长、短轴长及离心率;
(2)若∠F1PF2=60°,求|PF1|•|PF2|的值.
| x2 |
| 25 |
| y2 |
| 16 |
(1)求椭圆的顶点坐标,长轴长、短轴长及离心率;
(2)若∠F1PF2=60°,求|PF1|•|PF2|的值.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出椭圆的a,b,c,运用离心率公式,即可得到椭圆的顶点坐标,长轴长、短轴长及离心率;
(2)运用余弦定理和椭圆的定义,结合配方,即可得到所求值.
(2)运用余弦定理和椭圆的定义,结合配方,即可得到所求值.
解答:
解:(1)椭圆
+
=1的a=5,b=4,则c=
=3,
则椭圆的顶点坐标为(5,0),(-5,0),(0,4),(0,-4),
长轴长10,短轴长8,及离心率e=
=
;
(2)由于|PF1|+|PF2|=2a=10,
在△PF1F2中,cos60°=
=
=
-1=
,
即有|PF1|•|PF2|=
.
| x2 |
| 25 |
| y2 |
| 16 |
| a2-b2 |
则椭圆的顶点坐标为(5,0),(-5,0),(0,4),(0,-4),
长轴长10,短轴长8,及离心率e=
| c |
| a |
| 3 |
| 5 |
(2)由于|PF1|+|PF2|=2a=10,
在△PF1F2中,cos60°=
| |PF1|2+|PF2|2-|F1F2|2 |
| 2|PF1|•|PF2| |
=
| (|PF1|+|PF2|)2-2|PF1|•|PF2|-4c2 |
| 2|PF1|•|PF2| |
=
| 4a2-4c2 |
| 2|PF1|•|PF2| |
| 1 |
| 2 |
即有|PF1|•|PF2|=
| 64 |
| 3 |
点评:本题考查椭圆的定义、方程和性质,考查余弦定理及运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
若f(x)=x5+2x3+3x2+x+1,用秦九韶算法计算f(3)=( )
| A、327 | B、328 |
| C、165 | D、166 |
已知函数f(x)=
,若f(2-a)>f(a),则实数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,1) |
| C、(1,2) |
| D、(-∞,-1) |
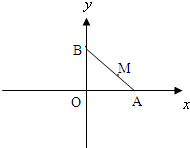 如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,|AB|=3,点M是线段AB上一点,且|AM|=1点M随线段AB的滑动而运动.
如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,|AB|=3,点M是线段AB上一点,且|AM|=1点M随线段AB的滑动而运动.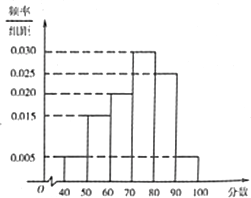 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为