题目内容
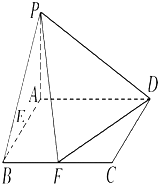 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.(1)证明:PF⊥FD;
(2)在线段PA上是否存在点G,使得EG∥平面PFD,若存在,确定点G的位置;若不存在,说明理由.
考点:直线与平面平行的性质,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)利用线面垂直的判定定理,先证明DF⊥平面PAF,即可得出结论;
(2)过点E作EH∥FD,交AD于点H,则EH∥平面PFD,且AH=
AD,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
AP,从而平面GEH∥平面PFD,即可得出结论.
(2)过点E作EH∥FD,交AD于点H,则EH∥平面PFD,且AH=
| 1 |
| 4 |
| 1 |
| 4 |
解答:
(1)证明:连接AF,则AF=
,DF=
,
∵AD=2,
∴AF2+DF2=AD2
∴AF⊥DF,
∵PA丄平面ABCD,
∴PA⊥DF,
∵PA∩AF=A
∴DF⊥平面PAF,
∵PF?平面PAF,
∴PF⊥FD.
(2)解:过点E作EH∥FD,交AD于点H,则EH∥平面PFD,且AH=
AD.
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
AP,
∴平面GEH∥平面PFD.
∵EG?平面GEH,
∴EG∥平面PFD.
从而满足AG=
AP的点G为所求.
| 2 |
| 2 |
∵AD=2,
∴AF2+DF2=AD2
∴AF⊥DF,
∵PA丄平面ABCD,
∴PA⊥DF,
∵PA∩AF=A

∴DF⊥平面PAF,
∵PF?平面PAF,
∴PF⊥FD.
(2)解:过点E作EH∥FD,交AD于点H,则EH∥平面PFD,且AH=
| 1 |
| 4 |
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
| 1 |
| 4 |
∴平面GEH∥平面PFD.
∵EG?平面GEH,
∴EG∥平面PFD.
从而满足AG=
| 1 |
| 4 |
点评:本题考查线面垂直,线面平行,考查学生分析解决问题的能力,正确运用线面垂直,线面平行的判定定理是关键.

练习册系列答案
相关题目
已知集合U={-1,0,1,2,3},P={-1,2,3},则∁UP=( )
| A、{0,1} |
| B、{-1,0,1} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
已知函数f(x)=
,若f(2-a)>f(a),则实数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,1) |
| C、(1,2) |
| D、(-∞,-1) |
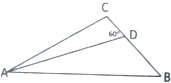 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎篷.AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点之间的连线段的D处,且∠ADC=60°.问多多与Feyman相距
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎篷.AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点之间的连线段的D处,且∠ADC=60°.问多多与Feyman相距