题目内容
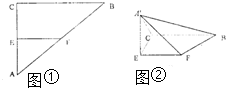
如图1,已知梯形ABCD,AB∥CD,且CD=2AB,E是CD边上的中点,线段AE与BD交于点F.将△ADE沿AE翻折到△AD′E位置,连接D′B和D′C(如图2).

(Ⅰ)若G是BC中点,求证:EG∥平面BD′F;
(Ⅱ)若AD=BC=AB=2,平面AD′E⊥平面ABCE,求三棱锥D′-BCE的体积.

(Ⅰ)若G是BC中点,求证:EG∥平面BD′F;
(Ⅱ)若AD=BC=AB=2,平面AD′E⊥平面ABCE,求三棱锥D′-BCE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:计算题,空间位置关系与距离
分析:(Ⅰ)利用线面平行的判定,EG∥BF,∴EG∥平面BD'F;
(Ⅱ)先证明D'F⊥平面ABCE,找到棱锥的高,代人体积公式计算.
(Ⅱ)先证明D'F⊥平面ABCE,找到棱锥的高,代人体积公式计算.
解答:
 解:(Ⅰ)证明:∵在图1中,E、G分别为DC,BC的中点,
解:(Ⅰ)证明:∵在图1中,E、G分别为DC,BC的中点,
∴EG∥BD,即EG∥BF.(3分)
∵EG?平面BD'F,BF?平面BD'F,
∴EG∥平面BD'F.(6分)
(Ⅱ)在图1中,∵AB∥DE,AB=DE,
∴四边形ABED为平行四边形.
∵AB=AD=2,
∴平行四边形ABED为菱形,
∴BD⊥AE,即D'F⊥AE,
∵平面AD'E⊥平面ABCE,且平面AD'E∩平面ABCE=AE,
∴D'F⊥平面ABCE.(9分)
∵BC=CE=BE=2,
∴S△BCE=
×22=
.(10分)
∴VD'-BCE=
•S△BCE•D′F=
×
×
=1.(13分)
 解:(Ⅰ)证明:∵在图1中,E、G分别为DC,BC的中点,
解:(Ⅰ)证明:∵在图1中,E、G分别为DC,BC的中点,∴EG∥BD,即EG∥BF.(3分)
∵EG?平面BD'F,BF?平面BD'F,
∴EG∥平面BD'F.(6分)
(Ⅱ)在图1中,∵AB∥DE,AB=DE,
∴四边形ABED为平行四边形.
∵AB=AD=2,
∴平行四边形ABED为菱形,
∴BD⊥AE,即D'F⊥AE,
∵平面AD'E⊥平面ABCE,且平面AD'E∩平面ABCE=AE,
∴D'F⊥平面ABCE.(9分)
∵BC=CE=BE=2,
∴S△BCE=
| ||
| 4 |
| 3 |
∴VD'-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,其中(2)的关键是判断出棱锥的高和底面面积,考查空间想象能力,计算能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
椭圆
+
=1的离心率为( )
| x2 |
| 100 |
| y2 |
| 36 |
A、
| ||
B、
| ||
C、
| ||
D、
|
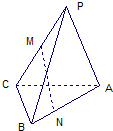 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.