题目内容
17.二项式${(\frac{2}{x}+x)^4}$的展开式中常数项为24.分析 根据二项式展开式的通项公式,令x的指数为0求出r的值,从而求出展开式中常数项.
解答 解:二项式${(\frac{2}{x}+x)^4}$展开式的通项公式为:
Tr+1=${C}_{4}^{r}$•${(\frac{2}{x})}^{4-r}$•xr=24-r•${C}_{4}^{r}$•x2r-4,
令2r-4=0,解得r=2,
∴展开式中常数项为T3=22•${C}_{4}^{2}$=24.
故答案为:24.
点评 本题考查了利用二项式展开式的通项公式求常数项的应用问题,是基础题.

练习册系列答案
相关题目
8.若i为虚数单位,则复数$\frac{1+i}{3-i}$等于( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{4}+\frac{1}{2}i$ | C. | $\frac{2}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
12.(x+1)5(x-2)的展开式中x2的系数为( )
| A. | 25 | B. | 5 | C. | -15 | D. | -20 |
2.设圆:x2+y2+2y-3=0与y轴交于A(0,y1),B(0,y2)两点,则y1y2 的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
9.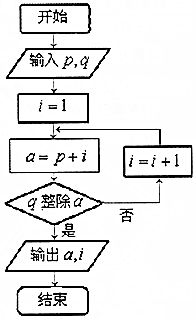 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )| A. | a=3,i=1 | B. | a=18,i=16 | C. | a=18,i=15 | D. | a=9,i=7 |
6.设等差数列{an}的前n项和为Sn,若S9=54,则a2+a4+a9=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 36 |
7.设p:x2-x<1,$q:{log_2}({x^2}-x)<0$,则非p是非q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |