题目内容
5.已知点A(a,b)与点B(0,3)在直线3x-4y+5=0的同侧,给出下列四个命题:①若a>1,则b>2;
②$\sqrt{{a}^{2}+{b}^{2}}$>1;
③函数f(x)=sinx-3a+4b-4有无数个零点;
④当b<0时,$\frac{b-1}{a}$的取值范围是(0,$\frac{3}{4}$).
其中所有正确命题的序号是①②④.
分析 点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,则(3a-4b+5)×(3×0-4×3+5)>0,即3a-4b+5<0,作出点A(a,b) 对应的平面区域,利用目标函数的几何意义结合数形结合进行判断即可
解答 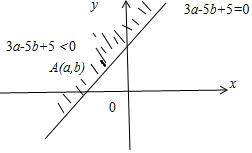 解:点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,
解:点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,
则(3a-4b+5)×(3×0-4×3+5)>0,即3a-4b+5<0,点A(a,b)的区域如图所示.
对于①,若a>1,由3a-4b+5<0;可得b>2,故正确;
对于②,∵原点到直线3a-4b+5=0的距离等于1,∴$\sqrt{{a}^{2}+{b}^{2}}$>1,故正确;
对于③,函数f(x)=sinx-3a+4b-4零点,就是y=sinx与y=3a-4b+4的交点,∵y=3a-4b+4>-1,故错;
对于④,当b<0时,$\frac{b-1}{a}$表示过点A(a,b)与点(0,1)的斜率,根据图象可得其取值范围是(0,$\frac{3}{4}$),故正确.
故答案为:①②④.
点评 本题考查的知识点是二元一次不等式与平面区域,考查转化思想与运算能力,属于基础题.

练习册系列答案
相关题目
15.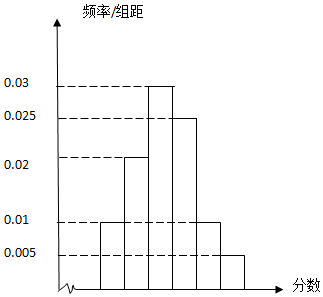 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
(I)用每组区间的中点值代表该组的数据,估算这批考生的平均成绩;
(II)现从及格的学生中,用分层抽样的方法抽取了70名学生(其中女生有34名),已知成绩“优异”(超过90分)的女生有1名,能否有95%的把握认为数学成绩优异与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示(I)用每组区间的中点值代表该组的数据,估算这批考生的平均成绩;
(II)现从及格的学生中,用分层抽样的方法抽取了70名学生(其中女生有34名),已知成绩“优异”(超过90分)的女生有1名,能否有95%的把握认为数学成绩优异与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
16.已知命题p:?x∈R,x2-2xsinθ+1≥0;命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,则下列命题中的真命题为( )
| A. | (¬p)∧q | B. | p∧(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
13.已知函数$f(x)=\left\{\begin{array}{l}{a^x},\;0<x≤1\;\\{log_a}x\;,x>1\end{array}\right.$(a>0且a≠1),若f(3a2)>f(1-2a),则a的取值范围是( )
| A. | $0<a<\frac{1}{2}$ | B. | $\frac{1}{3}<a<\frac{1}{2}$ | C. | $0<a<\frac{1}{3}$ | D. | a>1或$0<a<\frac{1}{3}$ |
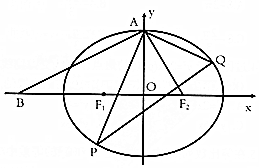 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足$\overrightarrow{B{F}_{1}}$=$\overrightarrow{{F}_{1}{F}_{2}}$,且$\overrightarrow{AB}$•$\overrightarrow{A{F}_{2}}$=0.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足$\overrightarrow{B{F}_{1}}$=$\overrightarrow{{F}_{1}{F}_{2}}$,且$\overrightarrow{AB}$•$\overrightarrow{A{F}_{2}}$=0. 若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )
若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )