题目内容
11.函数y=ex(2x-1)的大致图象是( )| A. | 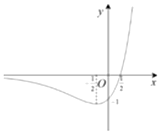 | B. | 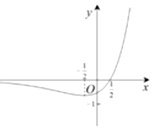 | ||
| C. | 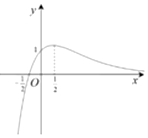 | D. | 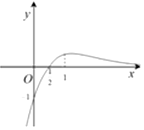 |
分析 判断函数的单调性,计算函数与坐标轴的交点坐标即可得出答案.
解答 解:y′=ex(2x-1)+2ex=ex(2x+1),
令y′=0得x=-$\frac{1}{2}$,
∴当x<-$\frac{1}{2}$时,y′<0,当x$>-\frac{1}{2}$时,y′>0,
∴y=ex(2x-1)在(-∞,-$\frac{1}{2}$)上单调递减,在(-$\frac{1}{2}$,+∞)上单调递增,
当x=0时,y=e0(0-1)=-1,∴函数图象与y轴交于点(0,-1);
令y=ex(2x-1)=0得x=$\frac{1}{2}$,∴f(x)只有1个零点x=$\frac{1}{2}$,
当x$<\frac{1}{2}$时,y=ex(2x-1)<0,当x$>\frac{1}{2}$时,y=ex(2x-1)>0,
综上,函数图象为A.
故选A.
点评 本题考查了函数的图象判断,函数单调性、零点、极值的计算,属于中档题.

练习册系列答案
相关题目
2.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为( )
| A. | $\frac{2\sqrt{2}π}{3}$ | B. | $\frac{\sqrt{2}π}{3}$ | C. | $\frac{2\sqrt{3}π}{3}$ | D. | $\frac{\sqrt{3}π}{3}$ |
6.${∫}_{0}^{1}$xdx=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -$\frac{1}{2}$ |
20.已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{π}{6}$)-$\frac{1}{2}$(ω>0),函数图象的对称中心到对称轴的最小距离为$\frac{π}{4}$,将函数f(x)的图象向右平移$\frac{π}{12}$个单位长度得到函数g(x)的图象,若g(x)-3≤m≤g(x)+3在x∈[0,$\frac{π}{3}$]上恒成立,则实数m的取值范围是( )
| A. | [-2,1] | B. | [-5,1] | C. | [-2,4] | D. | [-5,4] |
1.已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$,则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=( )
| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |