题目内容
9.某程序框图如图所示,若输出的p值为31,则判断框内应填入的不等式是( )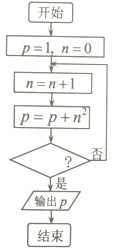
| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加计算p的值,条件框内的语句是决定是否结束循环,模拟执行程序即可得到答案.
解答 解:模拟程序的运行,可得
p=1,n=0
执行循环体,n=1,p=1+12=2,
不满足条件,执行循环体,n=2,p=2+22=6,
不满足条件,执行循环体,n=3,p=6+32=15,
不满足条件,执行循环体,n=4,p=15+42=31,
由题意,此时应该满足条件,退出循环,输出p的值为31,
则判断框内应填入的不等式是n>3.
故选:B.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20.已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{π}{6}$)-$\frac{1}{2}$(ω>0),函数图象的对称中心到对称轴的最小距离为$\frac{π}{4}$,将函数f(x)的图象向右平移$\frac{π}{12}$个单位长度得到函数g(x)的图象,若g(x)-3≤m≤g(x)+3在x∈[0,$\frac{π}{3}$]上恒成立,则实数m的取值范围是( )
| A. | [-2,1] | B. | [-5,1] | C. | [-2,4] | D. | [-5,4] |
17.有下述说法:①a>b>0是a2>b2的充分不必要条件.②a>b>0是$\frac{1}{a}<\frac{1}{b}$的充要条件.③a>b>0是a3>b3的充要条件.则其中正确的说法有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.某年级举办团知识竞赛A、B、C、D四个班报名人数如下:
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
(I )求各班参加竞赛的人数:
(II) 若B班每位参加竞赛的同学对每个题目答对的概率均为p,求B班恰好有2位同学获得奖品的概率;
(III) 若这10个题目,小张同学只有2个答不对,记小张答对的题目数为X,求X的分布列及数学期望E(X)
1.已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$,则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=( )
| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |
18.已知平面α及直线a,b,则下列说法正确的是( )
| A. | 若直线a,b与平面α所成角都是30°,则这两条直线平行 | |
| B. | 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直 | |
| C. | 若直线a,b平行,则这两条直线中至少有一条与平面α平行 | |
| D. | 若直线a,b垂直,则这两条直线与平面α不可能都垂直 |