题目内容
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
分析 由已知条件,分别求出抛物线的准线方程和双曲线的渐近线,由三角形的面积求出b=2$\sqrt{3}$a,由此能求出双曲线的离心率.
解答 解:y2=4x的准线方程为l:x=-1,
∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,△ABO的面积为2$\sqrt{3}$,
∴$\frac{1}{2}$×1×$\frac{2b}{a}$=2$\sqrt{3}$,
∴b=2$\sqrt{3}$a,
∴c=$\sqrt{13}$a,
∴e=$\sqrt{13}$
故选:D
点评 本题考查双曲线的离心率的求法,是中档题,解题时要熟练掌握抛物线、双曲线的简单性质.

练习册系列答案
相关题目
1.已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$,则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=( )
| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |
6.已知平面向量$\overrightarrow a$和$\overrightarrow b$的夹角为60°,$\overrightarrow a=(2,0)$,$|\overrightarrow b|=1$,则$|\overrightarrow a+2\overrightarrow b|$=( )
| A. | 20 | B. | 12 | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
4.已知点P(1,-2),O(0,0),点M(x,y)满足不等式组$\left\{\begin{array}{l}{x+y≤6}\\{y-2x≤3}\\{y≥0}\\{x≥0}\end{array}\right.$,则z=$\overrightarrow{OP}$$•\overrightarrow{PM}$的取值范围为( )
| A. | [-1,14] | B. | [-14,1] | C. | [-2,13] | D. | [-13,2] |
2.某小卖部销售某品牌的饮料的零售价与销量间的关系统计如下:
已知x,y的关系符合回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=-20.若该品牌的饮料的进价为2元,为使利润最大,零售价应定为3.75元.
| 单价x(元) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
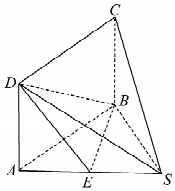 如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.
如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.