题目内容
4.已知M、N是焦点为F的抛物线y2=4x上两个不同点,且线段MN的中点A的横坐标是3,直线MN与x轴交于点B,则点B的横坐标的取值范围是( )| A. | (-3,3] | B. | (-∞,3] | C. | (-6,-3] | D. | (-6,3) |
分析 设M(x1,y1),N(x2,y2),A(3,y0).设直线MN的方程为:my=x+t,与抛物线方程联立化为:y2-4my+4t=0,△>0,即t<m2.利用根与系数的关系、中点坐标公式可得y0=2m.可得3+t=2m2,可得xB=-t=-2m2+3,即可得出.
解答 解:设M(x1,y1),N(x2,y2),A(3,y0).
设直线MN的方程为:my=x+t,
联立$\left\{\begin{array}{l}{my=x+t}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-4my+4t=0,
△=16m2-16t>0,即t<m2.
y1+y2=4m,∴y0=2m.
∴3+t=2m2,
∴xB=-t=-2m2+3≤3,
又t<m2,可得-2m2+3>-m2,解得m2<3,
∴xB=-t=-2m2+3>-3,
∴xB=-2m2+3∈(-3,3].
故选:A.
点评 本本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题、中点坐标公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
20.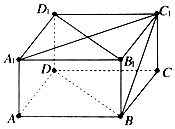 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{10}$ |
19.已知a,b∈R,则命题“若a+b=1,则a2+b2≥$\frac{1}{2}$”的逆否命题是( )
| A. | 若a+b≠1,则a2+b2<$\frac{1}{2}$ | B. | 若a+b=1,则a2+b2<$\frac{1}{2}$ | ||
| C. | 若a2+b2<$\frac{1}{2}$,则a+b≠1 | D. | 若a2+b2≥$\frac{1}{2}$,则a+b=1 |
13.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{(\frac{1}{3})^{x}-2,x≤0}\end{array}\right.$,则不等式f(x)≥1的解集为( )
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
14.如图,正三棱柱(底面为正三角形,侧棱垂直底面)的正视图面积a2,则侧视图的面积为( )
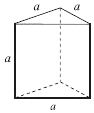

| A. | a2 | B. | $\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\sqrt{3}{a^2}$ | D. | $\frac{{\sqrt{3}}}{4}{a^2}$ |
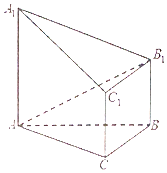 如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.
如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.