题目内容
已知f(x)+2f(x-1)=2x,求f(x).
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由题意,f(x)是一次函数,设出解析式,代入题目中的关系式,即可求出答案.
解答:
解:∵f(x)+2f(x-1)=2x,
∴f(x)是一次函数,
设f(x)=ax+b,
则f(x)+2f(x-1)=(ax+b)+2[a(x-1)+b]=3ax+3b-2a=2x;
∴
,
解得a=
,b=
;
∴f(x)=
x+
.
∴f(x)是一次函数,
设f(x)=ax+b,
则f(x)+2f(x-1)=(ax+b)+2[a(x-1)+b]=3ax+3b-2a=2x;
∴
|
解得a=
| 2 |
| 3 |
| 4 |
| 9 |
∴f(x)=
| 2 |
| 3 |
| 4 |
| 9 |
点评:本题考查了求函数解析式的问题,解题时应根据题意,得出f(x)是一次函数,是解题的关键.

练习册系列答案
相关题目
设复数z=a-bi(a,b∈R)且a+bi=
,则复数z在复平面所对应的点位于( )
| 11-7i |
| (1-i)2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
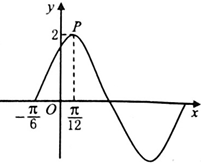 已知函数
已知函数