Question

关于x的方程

3

sin2x+cos2x=k+1在[0，

π

2

]内有相异的两个实数根x₁，x₂，求实数k的取值范围及x₁+x₂的值．

Answer 1

考点：两角和与差的正弦函数,正弦函数的图象

专题：三角函数的图像与性质

分析：利用两角和差的正弦公式可把方程

3

sin2x+cos2x=k+1化为sin(2x+

π

6

)=

k+1

2

，分别画出图象：f（x）=sin(2x+

π

6

)，y=

k+1

2

．则方程

3

sin2x+cos2x=k+1在[0，

π

2

]内有相异的两个实数根x₁，x₂，?函数y=f（x）与y=

k+1

2

有两个不同的交点，可得

1

2

≤

k+1

2

＜1．由图象可知：当x∈[0，

π

3

]时，函数y=f（x）的图象关于直线x=

π

6

对称．

解答： 解：方程

3

sin2x+cos2x=k+1化为2(

3

2

sin2x+

1

2

cos2x)=k+1，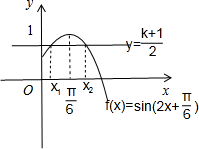
∴sin(2x+

π

6

)=

k+1

2

，
∵x∈[0，

π

2

]，∴(2x+

π

6

)∈[

π

6

，

7π

6

]，
画出图象：f（x）=sin(2x+

π

6

)，y=

k+1

2

．
当0≤x≤

π

6

时，f（x）∈[

1

2

，1]；
当

π

6

＜x≤

π

2

时，f（x）∈[-

1

2

，1)．
方程

3

sin2x+cos2x=k+1在[0，

π

2

]内有相异的两个实数根x₁，x₂，?函数y=f（x）与y=

k+1

2

有两个不同的交点，
∴

1

2

≤

k+1

2

＜1，解得0≤k＜1．
由图象可知：当x∈[0，

π

3

]时，函数y=f（x）的图象关于直线x=

π

6

对称．
∴x1+x2=2×

π

6

=

π

3

．

点评：本题考查了两角和差的正弦公式、方程的实数根转化为图象的交点、正弦函数的轴对称性单调性有界性，属于中档题．