题目内容
5.在△ABC中,已知面积S=$\frac{1}{4}$(a2+b2-c2),则角C的度数为$\frac{π}{4}$.分析 由已知及三角形面积公式可求c2=a2+b2-2absinC,结合余弦定理可得sinC=cosC,根据范围C∈(0,π),可求C的值.
解答 解:∵S=$\frac{1}{4}$(a2+b2-c2)=$\frac{1}{2}$absinC,
∴a2+b2-c2=2absinC,
∴c2=a2+b2-2absinC,
∵由余弦定理可得:c2=a2+b2-2abcosC,
∴sinC=cosC,
∵C∈(0,π),
∴C=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题主要考查了三角形面积公式,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
 如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{\begin{array}{l}8\end{array}}$ | D. | $\frac{3}{4}$ |
13.已知n=$\frac{9}{4}$${∫}_{0}^{2}$x2dx,若(1+2x)n=a0+a1x+a2x2+a3x3+a4x4+…+anxn,则a0+a1+a3+a5=( )
| A. | 364 | B. | 365 | C. | 728 | D. | 730 |
20.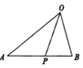 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
10.如果x-1+yi与i-3x是共轭复数(x,y是实数),则x+y=( )
| A. | -1 | B. | 1 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
17.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断是否有95%的把握认为“性别与休闲方式”有关系.
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据建立一个2×2列联表;
(2)判断是否有95%的把握认为“性别与休闲方式”有关系.
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(Χ2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
18.某同学在利用“五点法”作函数f(x)=Asin(ωx+Φ)+t的图象时,列出了如下表格中的部分数据
(1)请将表格补充完整,并写出f(x)的解析式;
(2)若x∈[-$\frac{5π}{12},\frac{π}{4}}$],求f(x)的最大值和最小值.
| x | $\frac{5π}{12}$ | $\frac{3π}{4}$ | |||
| ωx+Φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x) | 6 | -2 |
(2)若x∈[-$\frac{5π}{12},\frac{π}{4}}$],求f(x)的最大值和最小值.