题目内容
⊙M:(x+1)2+y2=1及⊙N:(x-1)2+y2=9,动圆P与⊙M外切且与⊙N相内切,圆心P的轨迹为曲线C
①求曲线C的方程;
②Q为曲线C上任一点,求
•
的取值范围.
①求曲线C的方程;
②Q为曲线C上任一点,求
| QM |
| QN |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:①利用两个圆相切的性质、双曲线的定义即可得出;
②利用数量积运算、双曲线的方程即可得出.
②利用数量积运算、双曲线的方程即可得出.
解答:
解:①|PM|-|PN|=1<|MN|=2,
∴圆心P的轨迹为双曲线的右支,其方程为
-
=1.(x>0).
②设Q(x,y)(
≤x≤
),
则
•
=(-1-x,-y)•(1-x,-y)=x2-1+y2
=4x2-
∈[
,
].
∴圆心P的轨迹为双曲线的右支,其方程为
| x2 | ||
|
| y2 | ||
|
②设Q(x,y)(
| 1 |
| 2 |
1+
| ||
| 4 |
则
| QM |
| QN |
=4x2-
| 1 |
| 4 |
| 3 |
| 4 |
15+
| ||
| 2 |
点评:本题考查了两个圆相切的性质、双曲线的定义及其方程、数量积运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )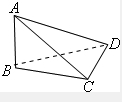

| A、1 | B、2 | C、3 | D、4 |
如表是一个2×2列联表:则表中a,b的值分别为( )
| y1 | y2 | 合计 | |
| x1 | a | 21 | 73 |
| x2 | 22 | 25 | 47 |
| 合计 | b | 46 | 120 |
| A、94,72 |
| B、52,50 |
| C、52,74 |
| D、74,52 |
已知2x+3y+4z=1,则x2+y2+z2的最小值是 ( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若(
+
)•(
-
)=0,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、正三角形 | B、直角三角形 |
| C、等腰三角形 | D、无法确定 |
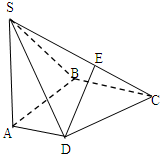 四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求:
四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求: