题目内容
已知椭圆
+
=1上一点P到它的右准线的距离为10，则点P到它的左焦点的距离是（ ）
| x2 |
| 100 |
| y2 |
| 36 |
| A、8 | B、10 | C、12 | D、14 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据椭圆的第二定义可知P到右焦点F的距离与其到右准线的距离之比为离心率，求出PF=8，即可求出点P到该椭圆的左焦点的距离．
解答：
解：椭圆
+
=1中a=10，b=6，∴c=8，∴e=
=
．
∵椭圆
+
=1上一点P到它的右准线的距离是10，
∴根据椭圆的第二定义可知P到右焦点F的距离与其到右准线的距离之比为离心率，即PF=8，
∴点P到该椭圆的左焦点的距离是2×10-8=12．
故选C．
| x2 |
| 100 |
| y2 |
| 36 |
| c |
| a |
| 4 |
| 5 |
∵椭圆
| x2 |
| 100 |
| y2 |
| 36 |
∴根据椭圆的第二定义可知P到右焦点F的距离与其到右准线的距离之比为离心率，即PF=8，
∴点P到该椭圆的左焦点的距离是2×10-8=12．
故选C．
点评：本题主要考查了椭圆的简单性质，解题的关键是灵活利用椭圆的第二定义、第一定义．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
y=sin（2x-
）-sin2x的一个单调递增区间是（ ）
| π |
| 3 |
A、[-
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
如图，已知AB⊥平面BCD，BC⊥CD，则图中直角三角形的个数为（ ）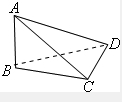
| A、1 | B、2 | C、3 | D、4 |
已知2x+3y+4z=1，则x2+y2+z2的最小值是 （ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直角三角形的周长为定值2l，则它的面积的最大值为（ ）
A、2
| ||
B、3
| ||
C、（3+2
| ||
D、（3-2
|
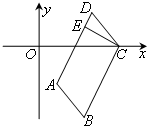如图，在平行四边形ABCD中，边AD所在直线方程为2x-y-2=0，顶点C（2，0）．