题目内容
已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由已知得f′(x)=-3x2+6x+9,由此能求出f(x)的单调区间.
(2)由f′(x)=-3x2+6x+9=0,得x=-1或x=3(舍),由此利用已知条件能求出它在区间[-2,2]上的最小值.
(2)由f′(x)=-3x2+6x+9=0,得x=-1或x=3(舍),由此利用已知条件能求出它在区间[-2,2]上的最小值.
解答:
解:(1)∵f(x)=-x3+3x2+9x+a,
∴f′(x)=-3x2+6x+9,
由f′(x)>0,得-1<x<3,
∴f(x)的单调递增区间为(-1,3);
由f′(x)<0,得x<-1或x>3,
∴f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)由f′(x)=-3x2+6x+9=0,得x=-1或x=3(舍),
∵f(-2)=8+12-18+a=2+a,
f(-1)=1+3-9+a=a-5,
f(2)=-8+12+18+a=22+a,
∵f(x)在区间[-2,2]上的最大值为20,
∴22+a=20,解得a=-2.
∴它在该区间上的最小值为a-5=-7.
∴f′(x)=-3x2+6x+9,
由f′(x)>0,得-1<x<3,
∴f(x)的单调递增区间为(-1,3);
由f′(x)<0,得x<-1或x>3,
∴f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)由f′(x)=-3x2+6x+9=0,得x=-1或x=3(舍),
∵f(-2)=8+12-18+a=2+a,
f(-1)=1+3-9+a=a-5,
f(2)=-8+12+18+a=22+a,
∵f(x)在区间[-2,2]上的最大值为20,
∴22+a=20,解得a=-2.
∴它在该区间上的最小值为a-5=-7.
点评:本题考查函数的单调区间的求法,考查函数在闭区间上的最小值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )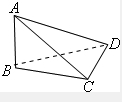

| A、1 | B、2 | C、3 | D、4 |
已知直角三角形的周长为定值2l,则它的面积的最大值为( )
A、2
| ||
B、3
| ||
C、(3+2
| ||
D、(3-2
|
在△ABC中,若(
+
)•(
-
)=0,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、正三角形 | B、直角三角形 |
| C、等腰三角形 | D、无法确定 |
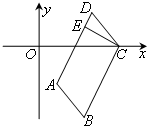 如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).
如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).