题目内容
不等式组
,表示的平面区域的面积是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:画出不等式组
表示的平面区域为等腰梯形及其内部的部分,求得A、B、C各个点的坐标,可得等腰梯形的面积.
|
解答:
 解:不等式组
解:不等式组
表示的平面区域如图所示的阴影部分:
容易求得A(0,1),B(1,2),C(2,2),
不等式组
表示的平面区域的面积是:
×2×2-
×1×1=
,
故答案为
.
 解:不等式组
解:不等式组
|
容易求得A(0,1),B(1,2),C(2,2),
不等式组
|
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为
| 3 |
| 2 |
点评:本题主要考查二元一次不等式组表示平面区域,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知空间四点A(4,1,3),B(2,3,1),C(3,7,-5),D(x,-1,3)共面,则x=( )
| A、4 | B、1 | C、10 | D、11 |
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )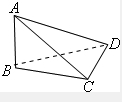

| A、1 | B、2 | C、3 | D、4 |
如表是一个2×2列联表:则表中a,b的值分别为( )
| y1 | y2 | 合计 | |
| x1 | a | 21 | 73 |
| x2 | 22 | 25 | 47 |
| 合计 | b | 46 | 120 |
| A、94,72 |
| B、52,50 |
| C、52,74 |
| D、74,52 |
已知2x+3y+4z=1,则x2+y2+z2的最小值是 ( )
A、
| ||
B、
| ||
C、
| ||
D、
|
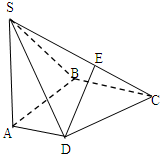 四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求:
四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求: