题目内容
已知向量
=(1,cos(ωx-
)),
=(
,
sin(ωx-
)),其中ω为常数,且ω>0
(1)若ω=1,且
∥
,求tanx的值;
(2)设函数f(x)=(
-
)2-(
-1)2,若f(x)的最小正周期为π,求f(x)在x∈(0,
)时的值域.
| a |
| π |
| 6 |
| b |
| 3 |
| 3 |
| π |
| 6 |
(1)若ω=1,且
| a |
| b |
(2)设函数f(x)=(
| a |
| b |
| 3 |
| π |
| 2 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:平面向量及应用
分析:(1)根据向量的运算得出tan(x-
)=1,运用tanx=tan[(x-
)+
]两角和正切公式即可.
(2)运用数量积得出f(x)=2-2sin(2x-
),根据三角函数性质求解得出-
<sin(2x-
)≤1,得出值域.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
(2)运用数量积得出f(x)=2-2sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
解答:
解:向量
=(1,cos(ωx-
)),
=(
,
sin(ωx-
)),其中ω为常数,且ω>0
(1)ω=1,向量
=(1,cos(x-
)),
=(
,
sin(x-
)),
∵
∥
,
∴
sin(x-
)-
cos(x-
)=0,
∴tan(x-
)=1,
∴tanx=tan[(x-
)+
]═
=
=2+
.
(2)f(x)=(
-
)2-(
-1)2=(1-
)2+(cos(ωx-
)-
sin(ωx-
))2-(
-1)2=2-2sin(2ωx-
),
∵f(x)的最小正周期为π,
∴ω=1,f(x)=2-2sin(2x-
),
∵0<x<
,
∴-
<2x-
<
,
∴-
<sin(2x-
)≤1,
∴0≤2-2sin(2x-
)<3,
故值域为[0,3),
| a |
| π |
| 6 |
| b |
| 3 |
| 3 |
| π |
| 6 |
(1)ω=1,向量
| a |
| π |
| 6 |
| b |
| 3 |
| 3 |
| π |
| 6 |
∵
| a |
| b |
∴
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
∴tan(x-
| π |
| 6 |
∴tanx=tan[(x-
| π |
| 6 |
| π |
| 6 |
1+
| ||||
1-1×
|
3+
| ||
3-
|
| 3 |
(2)f(x)=(
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
∵f(x)的最小正周期为π,
∴ω=1,f(x)=2-2sin(2x-
| π |
| 6 |
∵0<x<
| π |
| 2 |
∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴0≤2-2sin(2x-
| π |
| 6 |
故值域为[0,3),
点评:本题综合考查了向量,三角函数的运算性质,计算量大,属于中档题.

练习册系列答案
相关题目
方程(
)x+x-3=0的解的个数有( )
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
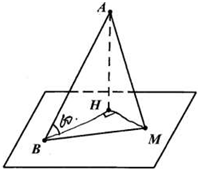 某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得
某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得