题目内容
已知椭圆
+
=1的右焦点为F，直线x+y-1=0和x+y+1=0与椭圆分别交于A、B和C、D四点，则|AF|+|BF|+|CF|+|DF|=（ ）
| x2 |
| 4 |
| y2 |
| 3 |
A、4
| ||
B、2
| ||
| C、8 | ||
| D、4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：画出图形，并设左焦点为F1，根据椭圆关于原点对称即可得到|AF1|=|DF|，|CF1|=|BF|，所以根据椭圆的定义便有：|AF|+|BF|+|CF|+|DF|=（|AF1|+|AF|）+（|CF1|+|CF|）=8．
解答：
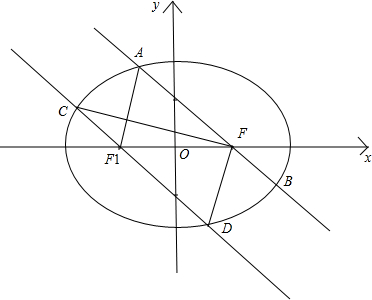解：如图所示，设椭圆的左焦点为F1，连接AF1；
根据椭圆关于原点对称可知四边形AF1DF为平行四边形；
∴|AF1|=|DF|，同理|CF1|=|BF|；
∴|AF|+|BF|+|CF|+|DF|=|AF|+|CF1|+|CF|+|AF1|=（|AF|+|AF1|）+（|CF1|+|CF|）=4a=8．
故选C．
解：如图所示，设椭圆的左焦点为F1，连接AF1；根据椭圆关于原点对称可知四边形AF1DF为平行四边形；
∴|AF1|=|DF|，同理|CF1|=|BF|；
∴|AF|+|BF|+|CF|+|DF|=|AF|+|CF1|+|CF|+|AF1|=（|AF|+|AF1|）+（|CF1|+|CF|）=4a=8．
故选C．
点评：考查椭圆的标准方程，椭圆的焦点，以及椭圆的对称性，椭圆的定义．
练习册系列答案
相关题目
复数1-i与1+bi的积是实数，则实数b的值是（ ）
| A、0 | B、1 | C、-1 | D、±1 |
函数y=log5-x（2x-3）的定义域为（ ）
A、(
| ||
B、(
| ||
| C、（4，5） | ||
D、(
|
已知f（x）=已知点F为抛物线C：y2=4x的焦点，点P为准线l上的动点，直线PF交抛物线C于A，B两点，若P的纵坐标为m（m≠0），点D为准线为l与x轴的交点，则△DAB的面积S的取值范围为（ ）
| A、（1，4） |
| B、（1，8） |
| C、（4，+∞） |
| D、（8，+∞） |
已知直线l：y=kx-2与抛物线 C：x2=-2py（p＞0）交于A、B两点，O为坐标原点