题目内容
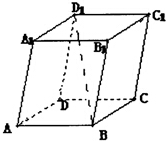
在平行六面体ABCD-A1B1C1D1中，用向量
，
，
来表示向量
为（ ）
| AB |
| AD |
| AA1 |
| BD1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点：向量加减混合运算及其几何意义
专题：空间向量及应用
分析：由向量的加减运算法则结合图象可得．
解答：
解：由题意可得
=
+
=
-
+
=
+
-
，
故选：B
| BD1 |
| BD |
| DD1 |
=
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
| AB |
故选：B
点评：本题考查向量的加减运算，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知a1=1，a2=-
，a3=-
，…，an+1=-
，…．那么a2014=（ ）
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| A、-2 | ||
B、-
| ||
| C、1 | ||
| D、2 |
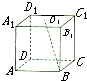如图，正方体A1B1C1D1-ABCD中，O1是上底面A1B1C1D1的中心，若正方体的棱长为2，则O1B与CD所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，D是直角△ABC斜边BC上一点，若AB=AD，AC=
DC，则sin∠ABD=（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若0＜α＜2π，则使sinα＜
和cosα＞
同时成立的α的取值范围是（ ）
| ||
| 2 |
| 1 |
| 2 |
A、（-
| ||||
B、（0，
| ||||
C、（
| ||||
D、（0，
|
已知两点O（0，0）、A（1，1）及直线l：x+y=a，它们满足：O、A有一点在直线l上或O、A在直线l的两侧．设h（a）=a2+2a+3，则使不等式x2+4x-2≤h（a）恒成立的x的取值范围是（ ）
| A、[0，2] |
| B、[-5，1] |
| C、[3，11] |
| D、[2，3] |
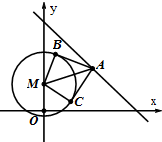已知圆M：x2+y2-2y=24，直线l：x+y=11，l上一点A的横坐标为a，过点A作圆M的两条切线l1，l2，切点分别为B，C．