题目内容
在极坐标系中,已知圆C的圆心为C(2,
),半径为1,求圆C的极坐标方程.
| π |
| 5 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:在圆C上任意取一点P(ρ,θ),在△POC中,由余弦定理可得1=4+ρ2-2×2×ρcos(θ-
),化简可得结果.
| π |
| 5 |
解答:
解:在圆C上任意取一点P(ρ,θ),在△POC中,由余弦定理可得
CP2=OC2+OP2-2OC•OP•cos∠POC,即1=4+ρ2-2×2×ρcos(θ-
),
化简可得 ρ2-4ρcos(θ-
)+3=0.
当O、P、C共线时,此方程也成立,故圆C的极坐标方程为 ρ2-4ρcos(θ-
)+3=0.
CP2=OC2+OP2-2OC•OP•cos∠POC,即1=4+ρ2-2×2×ρcos(θ-
| π |
| 5 |
化简可得 ρ2-4ρcos(θ-
| π |
| 5 |
当O、P、C共线时,此方程也成立,故圆C的极坐标方程为 ρ2-4ρcos(θ-
| π |
| 5 |
点评:本题主要考查求简单曲线的极坐标方程,余弦定理的应用,属于基础题.

练习册系列答案
相关题目
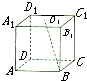 如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )
如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两点O(0,0)、A(1,1)及直线l:x+y=a,它们满足:O、A有一点在直线l上或O、A在直线l的两侧.设h(a)=a2+2a+3,则使不等式x2+4x-2≤h(a)恒成立的x的取值范围是( )
| A、[0,2] |
| B、[-5,1] |
| C、[3,11] |
| D、[2,3] |
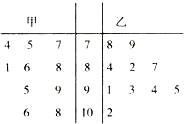 某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.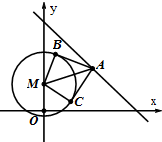 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.