题目内容
 如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点.(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)利用三角形中位线的性质,可得线线平行,证明EFGH为平行四边形,可得EF∥GH,进而可得线面平行;
(2)先证明线面垂直,再证明面面垂直即可.
(2)先证明线面垂直,再证明面面垂直即可.
解答:
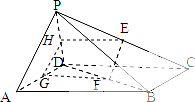 证明:(1)设PD中点为H,AD中点为G,连结FG,GH,HE,
证明:(1)设PD中点为H,AD中点为G,连结FG,GH,HE,
∵G为AD中点,F为BD中点,
∴GF∥AB且EF=
AB,
同理EH∥CD且EF=
CD,
∵ABCD为矩形,∴AB∥CD,AB=CD,
∴GF∥EH,GF=EH,
∴EFGH为平行四边形,∴EF∥GH,
又∵GH?面PAD,EF?面PAD,∴EF∥面PAD.
(2)∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,
又∵ABCD为矩形,∴CD⊥AD,
∴CD⊥面PAD
又∵CD?面PCD,∴面PAD⊥面PCD.
 证明:(1)设PD中点为H,AD中点为G,连结FG,GH,HE,
证明:(1)设PD中点为H,AD中点为G,连结FG,GH,HE,∵G为AD中点,F为BD中点,
∴GF∥AB且EF=
| 1 |
| 2 |
同理EH∥CD且EF=
| 1 |
| 2 |
∵ABCD为矩形,∴AB∥CD,AB=CD,
∴GF∥EH,GF=EH,
∴EFGH为平行四边形,∴EF∥GH,
又∵GH?面PAD,EF?面PAD,∴EF∥面PAD.
(2)∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,
又∵ABCD为矩形,∴CD⊥AD,
∴CD⊥面PAD
又∵CD?面PCD,∴面PAD⊥面PCD.
点评:本题考查线面平行、面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
若直线l1:y=kx+1与l2:x-y-1=0的交点在第一象限内,则k的取值范围是( )
| A、k>1 |
| B、-1<k<1 |
| C、k<-1或k>1 |
| D、k<-1 |
如图,D是直角△ABC斜边BC上一点,若AB=AD,AC=
DC,则sin∠ABD=( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中,a14=
,a114=
,a2014=
,则ab+19bc-20ac=( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、0 | B、14 |
| C、114 | D、2014 |
已知两点O(0,0)、A(1,1)及直线l:x+y=a,它们满足:O、A有一点在直线l上或O、A在直线l的两侧.设h(a)=a2+2a+3,则使不等式x2+4x-2≤h(a)恒成立的x的取值范围是( )
| A、[0,2] |
| B、[-5,1] |
| C、[3,11] |
| D、[2,3] |
 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.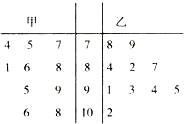 某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.