题目内容
设U=R,集合A={x|x2+4x+3=0},B={x|x2+(m+1)x+m=0}.若∁U(A)∩B=∅,则m的值是 .
考点:交、并、补集的混合运算
专题:集合
分析:求出A中方程的解确定出A,根据全集U=R求出A的补集,由A的补集与B的交集为空集,确定出m的值即可.
解答:
解:由A中方程解得:x=-1或x=-3,即A={-3,-1},
∵全集U=R,∴∁UA={x∈R|x≠-3或x≠-1},
∵B={x|x2+(m+1)x+m=0},且(∁UA)∩B=∅,
∴分三种情况考虑:①当B中方程仅有一个解x=-3时,m无解;
②当B中方程仅有一个解x=-1时,m=1;
③当B中方程有两个解时,m=3,
综上,m的值为1或3.
故答案为:1或3
∵全集U=R,∴∁UA={x∈R|x≠-3或x≠-1},
∵B={x|x2+(m+1)x+m=0},且(∁UA)∩B=∅,
∴分三种情况考虑:①当B中方程仅有一个解x=-3时,m无解;
②当B中方程仅有一个解x=-1时,m=1;
③当B中方程有两个解时,m=3,
综上,m的值为1或3.
故答案为:1或3
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
求证:
+
>
( )
| 2 |
| 3 |
| 5 |
| A、综合法 |
| B、分析法 |
| C、综合法、分析法配合使用 |
| D、间接证法 |
在直角坐标系中,方程(x+y-1)(
-y)=0所表示的曲线为( )
| 3+2x-x2 |
| A、一条直线和一个圆 |
| B、一条线段和一个圆 |
| C、一条直线和半个圆 |
| D、一条线段和半个圆 |
函数y=
的定义域为M,值域为N,则M∩N=( )
| 3x-2 |
| A、M | ||
| B、(1,+∞) | ||
C、(-∞,
| ||
| D、N |
方程
-
=1表示椭圆,则a的取值范围是( )
| x2 |
| 3 |
| y2 | ||
sin(2a+
|
A、-
| ||||
B、kπ-
| ||||
C、
| ||||
D、2kπ-
|
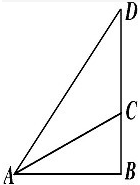 已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=
已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=