题目内容
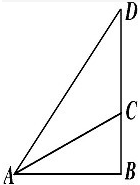 已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=
已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=| 1 |
| 2 |
考点:解三角形的实际应用
专题:计算题,解三角形
分析:分析题意可得,BC=20,通过直角三角形求BD,再求CD.
解答:
 解:由题意可知,
解:由题意可知,
BC=20,
∵tanα=
=
;
∴AB=40;
tan∠DAB=tan(45°+α)
=
=3;
故
=3;
则BD=120;
故CD=BD-BC=100(m);
即该电视塔高100m.
 解:由题意可知,
解:由题意可知,BC=20,
∵tanα=
| BC |
| AB |
| 1 |
| 2 |
∴AB=40;
tan∠DAB=tan(45°+α)
=
1+
| ||
1-
|
故
| BD |
| AB |
则BD=120;
故CD=BD-BC=100(m);
即该电视塔高100m.
点评:本题考查了解三角形的实际应用,利用到了三角恒变换及直角三角形中求值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知ξ~N(0,s2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
| A、0.477 |
| B、0.628 |
| C、0.954 |
| D、0.977 |
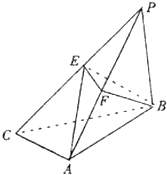 如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4
如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4