题目内容

斜率为1的直线与两直线2x+y-1=0，x+2y-2=0分别交于A、B两点，求线段AB中点的轨迹方程．
考点：轨迹方程
专题：计算题,直线与圆
分析：设A（x0，1-2x0）、B（2-2y0，y0），AB中点P（x，y），利用斜率为1及中点坐标公式，即可求线段AB中点的轨迹方程．
解答： 解：设A（x0，1-2x0）、B（2-2y0，y0），AB中点P（x，y），
则一方面
1-2x0-y0
x0-2+2y0
=1，∴x0+y0-1=0①
另一方面
x0+2-2y0=2x
1-2x0+y0=2y
，
∴
x0=-
2x+4y-4
3
y0=-
4x+2y-5
3
，
代入整理可得x+y-1=0．
点评：本题考查求线段AB中点的轨迹方程，考查代入法的运用，比较基础．
练习册系列答案
相关题目
设U=R，集合A={x|x2+4x+3=0}，B={x|x2+（m+1）x+m=0}．若∁U（A）∩B=∅，则m的值是
 
．
已知函数f（x）=blnx-ax+1（ab＞0）
（1）讨论f（x）在其定义域上的单调性．
（2）若b=1时，f（x）≤0恒成立，求实数a的取值范围．
设定义域为R的函数f（x）=
2x+1
a+4x
为偶函数，其中a为实常数．
（1）求a的值；
（2）求函数y=f（x）的值域．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右准线为x=
3
2
6
，离心率为
6
3
，A（-a，0），B（0，b），光线通过点C（-1，0）射到线段AB上的点T（端点除外），经过线段AB反射，其反射光线与椭圆交于点M．
（1）求椭圆的方程；
（2）若TC=TM，求T点横坐标m的值．
求证：sin2α+cosαcos（
π
3
+α）-sin2（
π
6
-α）的值是与α无关的定值．
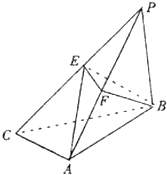如图，三棱锥P-ABC中，PB⊥底面ABC于B，∠BCA=90°，PB=BA=CA=4
2
，点E、F分别是PC和AP的中点
（1）求证：侧面PAC⊥侧面PBC；
（2）求点B到侧面PAC的距离；
（3）求二面角A-BE-F的大小．
已知一动圆P与圆M1：（x+4）2+y2=25和圆M2：（x-4）2+y2=1均外切（其中M1、M2分别为圆M1和圆M2的圆心）．
（Ⅰ）求动圆圆心P的轨迹E的方程；
（Ⅱ）若过点M2的直线l与曲线E有两个交点A、B，求|AM1|•|BM1|的取值范围．
已知函数f（x）=ax2+（1-2a）x-lnx（a∈R）．
（1）求函数f（x）的单调增区间；
（2）当a＜0时，求函数f（x）在区间[
1
2
，1]上最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网