题目内容
设函数g(x)=(x+1)ln(x+1)-x,f(x)=a(x+1)2•ln(x+1)+bx,曲线y=f(x)在原点(0,0)处的切线方程为y=0,且经过点(e-1,e2-e+1).
(1)求y=f(x)的表达式,并证明:当x≥0时,g(x)≥0;
(2)若当x≥0时,f(x)≥mx2恒成立,求实数m的取值范围.
(1)求y=f(x)的表达式,并证明:当x≥0时,g(x)≥0;
(2)若当x≥0时,f(x)≥mx2恒成立,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:分类讨论,导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(1)求出函数f(x)的导数,求得切线的斜率,再将点(e-1,e2-e+1)代入f(x)的解析式,解方程即可得到a,b,进而得到f(x)的解析式;
(2)令h(x)=f(x)-mx2=(x+1)2•ln(x+1)-x-mx2,求出h(x)的导数,对m讨论,当m≤
时,当m>
时,判断导数的符号,得到单调性即可求得m的范围.
(2)令h(x)=f(x)-mx2=(x+1)2•ln(x+1)-x-mx2,求出h(x)的导数,对m讨论,当m≤
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)解:f(x)=a(x+1)2•ln(x+1)+bx的导数为
f′(x)=2a(x+1)ln(x+1)+a(x+1)+b,
由曲线y=f(x)在原点(0,0)处的切线方程为y=0,即有a+b=0,
曲线y=f(x)经过点(e-1,e2-e+1),则ae2+b(e-1)=e2-e+1,
解得a=1,b=-1,
即有f(x)=(x+1)2•ln(x+1)-x.
证明:函数g(x)=(x+1)ln(x+1)-x的导数为g′(x)=ln(x+1)+1-1=ln(x+1),
当x≥0时,ln(x+1)≥0,即有g(x)在x≥0上递增,则g(x)≥g(0)成立;
(2)解:令h(x)=f(x)-mx2=(x+1)2•ln(x+1)-x-mx2,
h′(x)=f′(x)-2mx=2(x+1)ln(x+1)+(1-2m)x.
当m≤
时,当x≥0时,h′(x)≥0恒成立,即有f(x)≥mx2.
当m>
时,当x≥0时,h′(x)≥0不恒成立.
则有实数m的取值范围为(-∞,
].
f′(x)=2a(x+1)ln(x+1)+a(x+1)+b,
由曲线y=f(x)在原点(0,0)处的切线方程为y=0,即有a+b=0,
曲线y=f(x)经过点(e-1,e2-e+1),则ae2+b(e-1)=e2-e+1,
解得a=1,b=-1,
即有f(x)=(x+1)2•ln(x+1)-x.
证明:函数g(x)=(x+1)ln(x+1)-x的导数为g′(x)=ln(x+1)+1-1=ln(x+1),
当x≥0时,ln(x+1)≥0,即有g(x)在x≥0上递增,则g(x)≥g(0)成立;
(2)解:令h(x)=f(x)-mx2=(x+1)2•ln(x+1)-x-mx2,
h′(x)=f′(x)-2mx=2(x+1)ln(x+1)+(1-2m)x.
当m≤
| 1 |
| 2 |
当m>
| 1 |
| 2 |
则有实数m的取值范围为(-∞,
| 1 |
| 2 |
点评:本题考查导数的运用:求切线方程和单调区间,主要考查导数的几何意义和函数的单调性的运用,以及分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
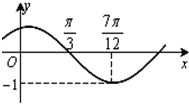 函数f(x)=sin(ωx+φ)(其中|φ|<
函数f(x)=sin(ωx+φ)(其中|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|