题目内容

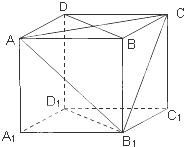如图，在棱长为1的正方体ABCD-A1B1C1D1中．
（1）求证：B1C∥平面AA1D1D；
（2）求三棱锥B-ACB1体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）根据正方体得出B1C∥A1D，再运用判定定理可证明．（2）利用三棱锥B-ACB1体积=三棱锥B1-ACB体积．求解就容易的多．
解答： （1）证明：∵在棱长为1的正方体ABCD-A1B1C1D1中．
∴B1C∥A1D，
∵B1C?平面AA1D1D；A1D?平面AA1D1D，
∴B1C∥平面AA1D1D；
（2）∵三棱锥B-ACB1体积=三棱锥B1-ACB体积．
∴V=
1
3
×
1
2
×1×1×1=
1
6

∴三棱锥B-ACB1体积为
1
6
．
点评：本题考查了空间几何体的体积的计算，运用转换顶点的方法，以及空间直线与平面的平行的判定，属于中档题．
练习册系列答案
相关题目
点A（1，-2），B（2，-3），C（3，10）是否在方程x2-xy+2y+1=0表示的曲线上？为什么？
已知两条不同的直线m，n，两个不同的平面α，β，在下列条件中可以得出α⊥β的是（　　）
A、m⊥n，n∥α，n∥β
B、m⊥n，α∩β=n，m?α
C、m∥n，n⊥β，m?α
D、m∥n，m⊥α，n⊥β
点A（sin215°，cos215°）在直角坐标平面上位于第
 
象限．
tan（-
17π
6
）=（　　）
A、
3
B、-
3
C、-
3
3
D、
3
3
已知cosα=-
3
5
，且α∈（π，
3π
2
），则cos
α
2
的值为
 
．
下列命题中，正确的是
 

（1）曲线y=lnx在点（1，0）处的切线方程是y=x-1；
（2）函数y=
16-2x
的值域是[0，4]；
（3）已知
a
=(sinθ，
1+cosθ
)，
b
=(1，
1-cosθ
)，其中θ∈(π，
3π
2
)，则
a
⊥
b
；
（4）O是△ABC所在平面上一定点，动点P满足：
OP
=
OA
+λ(
AB
sinC
+
AC
sinC
)，λ∈（0，+∞），则直线1过三角形的内心．
已知数列{an}（n∈N*），其前n项和为Sn，给出下列四个命题：
①若{an}是等差数列，则三点(10，
S10
10
)、(100，
S100
100
)、(110，
S110
110
)共线；
②若{an}是等差数列，且a1=-11，a3+a7=-6，则S1、S2、…、Sn这n个数中必然存在一个最大者；
③若{an}是等比数列，则Sm、S2m-Sm、S3m-S2m（m∈N*）也是等比数列；
④若Sn+1=a1+qSn（其中常数a1q≠0），则{an}是等比数列；
⑤若等比数列{an}的公比是q（q是常数），且a1=1，则数列{an2}的前n项和sn=
1-q2n
1-q2
．
其中正确命题的序号是
 
．（将你认为正确命题的序号都填上）
已知函数f（x）对一切实数x，y∈R都有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＜0，又f（3）=-2．
（1）试判定该函数的奇偶性；
（2）试判断该函数在R上的单调性；
（3）求f（x）在[-12，12]上的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网