题目内容
已知数列{an}中,前n项和为Sn,a1=5,且Sn+1=Sn+2an=2n+2(n∈N+).
(1)求a2,a3的值;
(2)设bn=
,若实数λ使得数列{bn}为等差数列,求λ的值.
(1)求a2,a3的值;
(2)设bn=
| an+λ |
| 2n |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)把已知递推式变形,得到an+1=2an+2n+2,然后最直接把a1=5代入依次求a2,a3的值;
(2)由an+1=2an+2n+2,得到
=
+
+
,把n依次取1,2,3,…,n后累加,求出数列{an}的通项公式,代入bn=
,由等差数列通项公式的特点求得λ的值.
(2)由an+1=2an+2n+2,得到
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
| an+λ |
| 2n |
解答:
解:(1)由Sn+1=Sn+2an+2n+2,得
Sn+1-Sn=2an+2n+2,即an+1=2an+2n+2,
∵a1=5,
∴a2=2a1+21+2=2×5+4=14.
a3=2a2+22+2=2×14+6=34;
(2)由(1)知,an+1=2an+2n+2,
∴
=
+
+
,
则
-
=
+
(n≥2),
由
-
=
+
,
-
=
+
,
-
=
+
,
…
-
=
+
(n≥2),
累加得:
-
=
(n-1)+(
+
+…+
),
即
=
+
(n-1)+
,
解得:an=(3+
-
)•2n(n≥2).
a1=5适合上式,
∴an=(3+
-
)•2n.
∴bn=
=
=3+
-
+
.
要使数列{bn}为等差数列,则
-
=
=0,即λ=2.
Sn+1-Sn=2an+2n+2,即an+1=2an+2n+2,
∵a1=5,
∴a2=2a1+21+2=2×5+4=14.
a3=2a2+22+2=2×14+6=34;
(2)由(1)知,an+1=2an+2n+2,
∴
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
则
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
由
| a2 |
| 22 |
| a1 |
| 21 |
| 1 |
| 2 |
| 1 |
| 2 |
| a3 |
| 23 |
| a2 |
| 22 |
| 1 |
| 2 |
| 1 |
| 22 |
| a4 |
| 24 |
| a3 |
| 23 |
| 1 |
| 2 |
| 1 |
| 23 |
…
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
累加得:
| an |
| 2n |
| a1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
即
| an |
| 2n |
| 5 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
解得:an=(3+
| n |
| 2 |
| 1 |
| 2n-1 |
a1=5适合上式,
∴an=(3+
| n |
| 2 |
| 1 |
| 2n-1 |
∴bn=
| an+λ |
| 2n |
(3+
| ||||
| 2n |
| n |
| 2 |
| 1 |
| 2n-1 |
| λ |
| 2n |
要使数列{bn}为等差数列,则
| λ |
| 2n |
| 1 |
| 2n-1 |
| λ-2 |
| 2n |
点评:本题考查数列递推式,考查了利用类加法求数列的通项公式,训练了等差关系的确定,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合P={x|y=x2},Q={y|y=x2},则下列关系正确的是( )
| A、P?Q | B、P=Q |
| C、P⊆Q | D、P?Q |
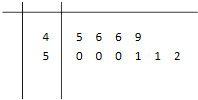 一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).
一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).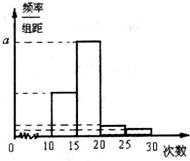 对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: