题目内容
已知sin2α+sinαcosα-2cos2α=0，则tanα= ．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边分母看做“1”，利用同角三角函数间的基本关系变形，再利用基本关系弦化切后即可求出tanα的值．
解答：
解：∵sin2α+sinαcosα-2cos2α=
=
=0，
∴tan2α+tanα-2=0，即（tanα-1）（tanα+2）=0，
解得：tanα=1或tanα=-2．
故答案为：1或-2
| sin2α+sinαcosα-2cos2α |
| sin2α+cos2α |
| tan2α+tanα-2 |
| tan2α+1 |
∴tan2α+tanα-2=0，即（tanα-1）（tanα+2）=0，
解得：tanα=1或tanα=-2．
故答案为：1或-2
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
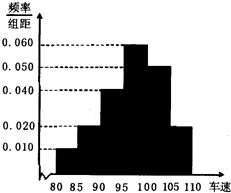2014年春节期间，高速公路车辆剧增．高管局侧控中心在一特定位置从七座以下小型汽车中按先后顺序，每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查，将它们的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105）．[105，110）后得到如图所示的频率分布直图．