题目内容
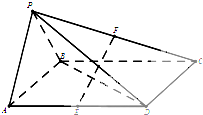 四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=| 1 |
| 2 |
(1)求证:EF∥平面PAB
(2)求证:EF⊥面PBD
(3)求三棱锥B-CDF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)取PB中点G,连接AG,FG,利用已知条件证明AEFG平行四边形,即可求证EF∥面PAB;
(2)利用已知条件通过直线与平面垂直的判定定理证明AG⊥面PBD,利用EF∥AG,证明EF⊥面PBD
(3)取AB中点M,连接PM,证明F到平面ABCD的距离h等于PM的一半,即可求出三棱锥B-CDF的体积.
(2)利用已知条件通过直线与平面垂直的判定定理证明AG⊥面PBD,利用EF∥AG,证明EF⊥面PBD
(3)取AB中点M,连接PM,证明F到平面ABCD的距离h等于PM的一半,即可求出三棱锥B-CDF的体积.
解答:
(1)证明:取PB中点G,连接AG,FG
又F分别为PC的中点.∴GF是△PBC的中位线,即GF∥BC,GF=
BC
又四边形ABCD底面是平行四边形,E分别为AB的中点,
∴AE∥BC,AE=
BC,
∴GF∥AE,GF=AE
∴四边形AEFG是平行四边形
∴EF∥AG,
又AG?平面PAB
∴EF∥平面PAB;
(2)证明:∵△PAB是等边三角形,AG⊥PB①
△ABD中,AD=2AB,∠BAD=60°,∴BD⊥AB,
∵面PAB⊥面ABCD,BD⊥AB,
∴DB⊥面PAB,∴DB⊥AG②
由 ①②可知,AG⊥PB,AG⊥BD,
∴AG⊥面PBD,
又EF∥AG,∴EF⊥面PBD;
(3)解:取AB中点M,连接PM,则
∵△PAB是等边三角形,
∴PM⊥AB,
∵面PAB⊥面ABCD,
∴PM⊥面ABCD,
∵F分别为PC的中点,
∴F到平面ABCD的距离h等于PM的一半,
∴h=
PM=
•
•1=
,
∴VB-CDF=VF-BCD=
S△BCDh=
.
又F分别为PC的中点.∴GF是△PBC的中位线,即GF∥BC,GF=
| 1 |
| 2 |
又四边形ABCD底面是平行四边形,E分别为AB的中点,
∴AE∥BC,AE=
| 1 |
| 2 |
∴GF∥AE,GF=AE
∴四边形AEFG是平行四边形
∴EF∥AG,
又AG?平面PAB
∴EF∥平面PAB;
(2)证明:∵△PAB是等边三角形,AG⊥PB①
△ABD中,AD=2AB,∠BAD=60°,∴BD⊥AB,
∵面PAB⊥面ABCD,BD⊥AB,
∴DB⊥面PAB,∴DB⊥AG②
由 ①②可知,AG⊥PB,AG⊥BD,
∴AG⊥面PBD,
又EF∥AG,∴EF⊥面PBD;
(3)解:取AB中点M,连接PM,则
∵△PAB是等边三角形,
∴PM⊥AB,
∵面PAB⊥面ABCD,
∴PM⊥面ABCD,
∵F分别为PC的中点,
∴F到平面ABCD的距离h等于PM的一半,
∴h=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴VB-CDF=VF-BCD=
| 1 |
| 3 |
| 1 |
| 8 |
点评:本题考查空间几何体中直线与平面平行的判定定理以及直线与平面垂直的判定定理的应用,三棱锥体积的计算,考查逻辑推理能力与计算能力.

练习册系列答案
相关题目
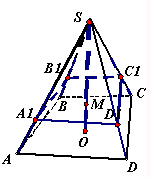 如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1
如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1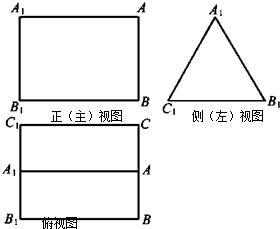 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.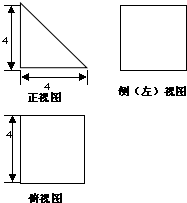 如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.
如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.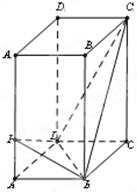 如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.