题目内容
以下公式中:①an=
[1-(-1)n];②an=
;③an=
,可以作为数列
,0,
,0,
,0,…通项公式的是( )
| ||
| 2 |
| 1-(-1)n |
|
| 2 |
| 2 |
| 2 |
| A、①② | B、②③ | C、①③ | D、①②③ |
考点:数列的概念及简单表示法
专题:探究型
分析:分析每一个公式的特点,结合已知数列中各项特点,对每一个公式进行验证,即可得出正确的结论.
解答:
解:对于①,n为奇数时,an=
×2=
;n为偶数时,an=
×0=0;∴an可以作为数列
,0,
,0,
,0,…的通项公式;
对于②,n为奇数时,an=
=
;n为偶数时,an=
=0;∴an可以作为数列
,0,
,0,
,0,…的通项公式;
对于③,n为奇数时,an=
;n为偶数时,an=0;∴an可以作为数列
,0,
,0,
,0,…的通项公式;
∴①②③都可以作为该数列的通项公式.
故选:D.
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
对于②,n为奇数时,an=
| 1-(-1) |
| 2 |
| 1-1 |
| 2 |
| 2 |
| 2 |
对于③,n为奇数时,an=
| 2 |
| 2 |
| 2 |
| 2 |
∴①②③都可以作为该数列的通项公式.
故选:D.
点评:本题考查了根据数列的前几项确定通项公式的问题,解题的关键是对每一个公式进行验证,判定是否满足条件,是基础题.

练习册系列答案
相关题目
设复数z1=1+i,z2=2+bi,若
为纯虚数,则实数b=( )
| z2 |
| z1 |
| A、2 | B、1 | C、-1 | D、-2 |
设数列{an}的前n项和为Sn,a1=1,an=
+2(n-1),(n∈N*),若S1+
+
+…+
-(n-1)2=2015,则n的值为( )
| Sn |
| n |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| A、1008 | B、1007 |
| C、2014 | D、2015 |
下列函数中,在区间(0,
)上为增函数的是( )
| π |
| 2 |
| A、y=sin2x |
| B、y=cosx |
| C、y=-cos2x |
| D、y=-tanx |
对空间任意两个向量
,
(
≠0),
∥
的充要条件是( )
| a |
| b |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若方程
+
=1表示的图形是双曲线,则k的取值范围为( )
| x2 |
| 2-k |
| y2 |
| k-1 |
| A、k>2或k<1 |
| B、1<k<2 |
| C、-2<k<1 |
| D、-1<k<2 |
设双曲线
-
=1上一点P,F1,F2是焦点,若|PF1|=10,则|PF2|等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、2 | B、2或18 | C、18 | D、16 |
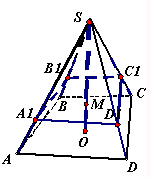 如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1
如图,在四棱锥S-ABCD中,SO⊥平面ABCD,O为垂足,点M在SO上,且SM:MO=2:1,经过点M作与底面ABCD平行的平面α,分别交棱SA、SB、SC、SD于A1、B1、C1、D1