题目内容
设数列{an}满足a1=2,an+1=an+3•2n-1.
(1)求数列{an}的通项公式an;
(2)令bn=n(an+1),求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式an;
(2)令bn=n(an+1),求数列{bn}的前n项和Sn.
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)利用数列的递推关系即可,求数列{an}的通项公式an;
(2)求出bn=n(an+1)的通项公式,利用错位相减法即可求数列{bn}的前n项和Sn.
(2)求出bn=n(an+1)的通项公式,利用错位相减法即可求数列{bn}的前n项和Sn.
解答:
解:(1)∵a1=2,an+1=an+3•2n-1.
∴an+1-an=3•2n-1.
即当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+3•20+3•21+3•22+…+3•2n-2.
=2+3×
=3×2n-1-1,n≥2,
当n=1时,也满足条件,
故数列{an}的通项公式an=3•2n-1-1
(2)∵bn=n(an+1)=3n×2n-1,
∴Sn=3(1•20+2•21+3•22+…+n•2n-1)
设x=1•20+2•21+3•22+…+n•2n-1 ①,
2x=1•21+2•22+3•23+…+(n-1)2n-1+n•2n②
①-②-x=1+21+22+23+…+2n-1-n•2n=1+
-n•2n=-1+(1-n)•2n
∴x=(n-1)•2n+1,
∴Sn=3(n-1)•2n+1.
∴an+1-an=3•2n-1.
即当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+3•20+3•21+3•22+…+3•2n-2.
=2+3×
| 1-2n-1 |
| 1-2 |
当n=1时,也满足条件,
故数列{an}的通项公式an=3•2n-1-1
(2)∵bn=n(an+1)=3n×2n-1,
∴Sn=3(1•20+2•21+3•22+…+n•2n-1)
设x=1•20+2•21+3•22+…+n•2n-1 ①,
2x=1•21+2•22+3•23+…+(n-1)2n-1+n•2n②
①-②-x=1+21+22+23+…+2n-1-n•2n=1+
| 2(1-2n-1) |
| 1-2 |
∴x=(n-1)•2n+1,
∴Sn=3(n-1)•2n+1.
点评:本题主要考查数列的通项公式的求法,以及利用错位相减法求数列的和,考查学生的运算能力.

练习册系列答案
相关题目
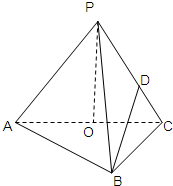 如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC. 如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=
如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=