题目内容
将标号分别为1、2、3、4、5五个小球分别放入红、黄、蓝、白、黑5个盒子里,每个盒子里只放1个小球.则1号球不在红盒内且2号球不在黄盒内的概率是 .
考点:计数原理的应用
专题:排列组合
分析:先由排列数公式计算将5个小球放入5个盒子中的情况数目,再求出1号球在红盒内,2号球在黄盒内有,1号既在红盒内且2号球也在黄盒内的种数,利用间接法,求出1号球不在红盒内且2号球不在黄盒内的种数,再根据概率公式计算即可.
解答:
解:将5个小球放入5个盒子中,有A55=120种放法,
其中1号球在红盒内有
=24种,2号球在黄盒内有
=24种,1号球在红盒内且2号球也在黄盒内有
=6种,
根据间接法,1号球不在红盒内且2号球不在黄盒内有120-24-24+6=78种,
故1号球不在红盒内且2号球不在黄盒内的概率P=
=
;
故选:
其中1号球在红盒内有
| A | 4 4 |
| A | 4 4 |
| A | 3 3 |
根据间接法,1号球不在红盒内且2号球不在黄盒内有120-24-24+6=78种,
故1号球不在红盒内且2号球不在黄盒内的概率P=
| 78 |
| 120 |
| 13 |
| 20 |
故选:
| 13 |
| 20 |
点评:本题主要考查了排列组合计算公式以及古典概率的计算公式,利用间接法是排列组合中常用的方法,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
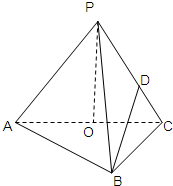 如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.