题目内容
8.已知向量$\overrightarrow{a}$=(x,1,2),$\overrightarrow{b}$=(1,y,-2),$\overrightarrow{c}$=(3,1,z),$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$⊥$\overrightarrow{c}$.(1)求向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$;
(2)求向量($\overrightarrow{a}$+$\overrightarrow{c}$)与($\overrightarrow{b}$+$\overrightarrow{c}$)所成角的余弦值.
分析 (1)根据空间向量的坐标表示与$\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{b}$⊥$\overrightarrow{c}$,列出方程组求出x、y、z的值即可;
(2)根据空间向量的坐标运算与数量积运算,利用公式求出($\overrightarrow{a}$+$\overrightarrow{c}$)与($\overrightarrow{b}$+$\overrightarrow{c}$)所成角的余弦值.
解答 解:(1)∵向量$\overrightarrow{a}$=(x,1,2),$\overrightarrow{b}$=(1,y,-2),$\overrightarrow{c}$=(3,1,z),
且$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$⊥$\overrightarrow{c}$,
∴$\left\{\begin{array}{l}{\frac{x}{1}=\frac{1}{y}=\frac{2}{-2}}\\{3+y-2z=0}\end{array}\right.$,
解得x=-1,y=-1,z=1;
∴向量$\overrightarrow{a}$=(-1,1,2),$\overrightarrow{b}$=(1,-1,-2),$\overrightarrow{c}$=(3,1,1);
(2)∵向量($\overrightarrow{a}$+$\overrightarrow{c}$)=(2,2,3),($\overrightarrow{b}$+$\overrightarrow{c}$)=(4,0,-1),
∴($\overrightarrow{a}$+$\overrightarrow{c}$)•($\overrightarrow{b}$+$\overrightarrow{c}$)=2×4+2×0+3×(-1)=5,
|$\overrightarrow{a}$+$\overrightarrow{c}$|=$\sqrt{{2}^{2}{+2}^{2}{+3}^{2}}$=$\sqrt{17}$,
|$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{{4}^{2}{+0}^{2}{+(-1)}^{2}}$=$\sqrt{17}$;
∴($\overrightarrow{a}$+$\overrightarrow{c}$)与($\overrightarrow{b}$+$\overrightarrow{c}$)所成角的余弦值为
cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{c})•(\overrightarrow{b}+\overrightarrow{c})}{|\overrightarrow{a}+\overrightarrow{c}|×|\overrightarrow{b}+\overrightarrow{c}|}$=$\frac{5}{\sqrt{17}×\sqrt{17}}$=$\frac{5}{17}$.
点评 本题考查了空间向量的坐标运算与数量积的应用问题,是基础题目.

| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
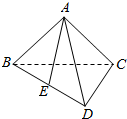 如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.
如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.