题目内容
6.某几何体的三视图如图所示,则该几何体的表面积为( )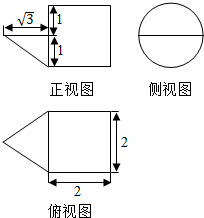
| A. | $\frac{13π}{2}+\sqrt{3}$ | B. | $\frac{(12+\sqrt{3})π}{6}$ | C. | $\frac{15π}{2}$ | D. | $\frac{(6+\sqrt{3})π}{3}$ |
分析 由已知中的三视图可得:该几何体是一个半圆锥和圆柱的组合体,求出各个面的面积相加可得答案.
解答 解:由已知中的三视图可得:该几何体是一个半圆锥和圆柱的组合体,
圆柱的底面半径为1,高为2,故底面积为:π,侧面积为4π,
半圆锥的底面半径为1,高为$\sqrt{3}$,故母线长为2,故侧面积为:π+$\sqrt{3}$,
故组合体的表面积为:π+4π+$\frac{1}{2}$π+π+$\sqrt{3}$=$\frac{13π}{2}+\sqrt{3}$,
故选:A
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
14.如果a>b>0,那么下列不等式成立的是( )
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )
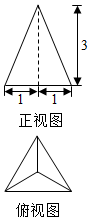

| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
15.已知M={(x,y)|x2+2y2=3},N={(x,y)|y=mx+b}.若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
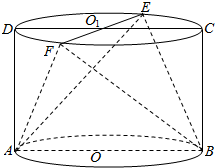 在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.