题目内容
1.函数f(x)=-4x3+6x2+1在[0,3]上的最大值为( )| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
分析 求函数的导数,判断函数的单调性和极值,从而求最值.
解答 解:∵f(x)=-4x3+6x2+1,
∴f′(x)=-12x2+12x=-12(x+1)(x-1);
由f′(x)=0得x=1或x=-1(舍),
当x∈[0,1),f′(x)>0;此时函数f(x)单调递增,
当x∈(1,3]时,f′(x)<0;此时函数f(x)单调递减,
即当x=1时,函数取得极大值同时也是最大值f(1)=-4+6+1=3,
故选:B
点评 本题考查了函数的最值的求法及导数的综合应用,求函数的导数,利用导数判断函数的单调性是解决本题的关键.,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )
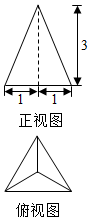

| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
12.已知函数f(x)=(m+2)x2+mx+1为偶函数,则f(x)在区间(1,+∞)上是( )
| A. | 先增后减 | B. | 先减后增 | C. | 减函数 | D. | 增函数 |
9.“x2-1>0”是“x>1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.下列函数中既是奇函数,又是区间(-1,0)上是减函数的( )
| A. | y=sinx | B. | y=-|x-1| | C. | y=ex-e-x | D. | y=ln$\frac{1-x}{1+x}$ |

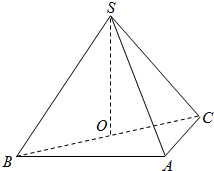 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.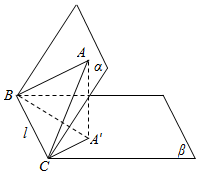 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.