题目内容
20.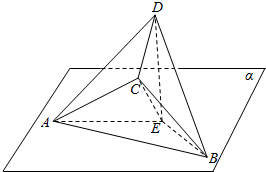 如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.
如图,三棱锥C-ABD的棱AB在平面α内,棱CD在平面α外,平面CAB⊥平面α,点D在平面α内的射影为E,且满足EA⊥EB,AC=BC=EA=EB=2,DE=2$\sqrt{2}$.(1)求证:AE∥平面BCD;
(2)求二面角E-CD-B的正弦值.
分析 (1)延长DC交平面α于F,连接AF,BF,EF,AB相交于G,利用线面平行的判定定理进行证明即可.
(2)建立空间坐标系,利用向量法进行求解即可.
解答 (1)证明:延长DC交平面α于F,连接AF,BF,EF,AB相交于G,
∵EA⊥EB,AC=BC=EA=EB,
∴△AEB≌△ACB,
则∠ACB=∠AEB=90°,
则AC⊥BC,
∵D在平面α内的射影为E,
∴DE⊥面ABE,
∵平面CAB⊥平面α,
∴DE∥平面CAB,
∵平面DEF∩平面ACB=CG,
∴DE∥CG,
∵AC=BC,∴G是AB的中点,
则四边形AEBF为正方形,则AE∥BF,
∵AE?平面BCD;BF?平面BCD;
∴AE∥平面BCD;
(2)建立以E为坐标原点的空间直角坐标系如图:
∵AC=BC=EA=EB=2,DE=2$\sqrt{2}$.
∴A(2,0,0),E(0,0,0),B(0,2,0),D(0,0,2$\sqrt{2}$),
G(1,1,0),F(2,2,0),
则$\overrightarrow{AG}$=(-1,1,0)为平面CED的一个法向量,
设$\overrightarrow{m}$=(x,y,z)是平面CDB即平面DFB的法向量,
则$\overrightarrow{DF}$=(2,2,-2$\sqrt{2}$),$\overrightarrow{BF}$=(2,0,0),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BF}=2x=0}\\{\overrightarrow{m}•\overrightarrow{DF}=2x+2y-2\sqrt{2}z=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x=0}\\{y=\sqrt{2}z}\end{array}\right.$,令z=1,则y=$\sqrt{2}$,
即$\overrightarrow{m}$=(0,$\sqrt{2}$,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{AG}$>=$\frac{\overrightarrow{m}•\overrightarrow{AG}}{|\overrightarrow{m}||\overrightarrow{AG}|}$=$\frac{\sqrt{2}}{\sqrt{2}•\sqrt{(\sqrt{2})^{2}+1}}=\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{AG}$>=$\sqrt{1-(\frac{\sqrt{3}}{3})^{2}}=\sqrt{1-\frac{3}{9}}=\sqrt{\frac{6}{9}}$=$\frac{\sqrt{6}}{3}$
即二面角E-CD-B的正弦值是$\frac{\sqrt{6}}{3}$.
点评 本题主要考查线面平行的证明以及空间角的求解,根据条件建立空间直角坐标系,利用向量法是解决空间角常用的方法,考查学生的运算和推理能力,综合性较强,难度较大.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案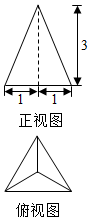
| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
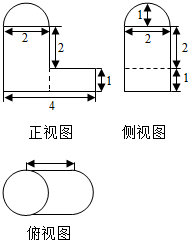
| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
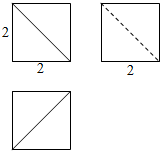 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
| A. | 先增后减 | B. | 先减后增 | C. | 减函数 | D. | 增函数 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |