题目内容
命题“?x＞0，x2-4x+2＞0”的否定是 ．
考点：命题的否定
专题：简易逻辑
分析：特称命题的否定是全称命题写出结果即可．
解答：
解：特称命题的否定是全称命题，
所以命题“?x＞0，x2-4x+2＞0”的否定是：?x＞0，x2-4x+2≤0．
故答案为：?x＞0，x2-4x+2≤0．
所以命题“?x＞0，x2-4x+2＞0”的否定是：?x＞0，x2-4x+2≤0．
故答案为：?x＞0，x2-4x+2≤0．
点评：本题考查命题的否定，注意特称命题与全称命题的否定关系．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
有一段“三段论”推理：对于可导函数f（x），若f（x）在区间（a，b）上是增函数，则f′（x）＞0对x∈（a，b）恒成立，因为函数f（x）=x3在R上是增函数，所以f（x）=3x2＞0对x∈R恒成立．以上推理中（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、推理正确 |
当λ变化时，直线λx-y+2+λ=0经过的定点是（ ）
| A、（1，2） |
| B、（-1，2） |
| C、（1，-2） |
| D、（-1，-2） |
如图，在正方体ABCD-A1B1C1D1中，E为AB中点，设I为全集，集合M，N，P都是其子集，则图中的阴影部分表示的集合为（ ）
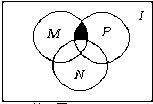
| A、M∩（N∪P） |
| B、M∩（P∩∁IN） |
| C、P∩（∁IN∩∁IM ） |
| D、（M∩N）∪（M∩P） |