Question

下列四个命题中
①设A，B两个定点，若|

PA

|-|

PB

|=3，则动点P的轨迹为双曲线．
②过定圆C上一定点A作圆的动弦A，B，O为原点，若

OP

=

1

2

（

OA

+

OB

），则动点P的轨迹为椭圆．
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率．
④双曲线

x2

25

-

y2

9

=1与椭圆

x2

35

+y²=1有相同的焦点，
其中真命题的序号为

 

（写出所有真命题的序号）

Answer 1

考点：命题的真假判断与应用

专题：圆锥曲线的定义、性质与方程

分析：利用双曲线的定义可判断①的正误；
不妨令定圆C的圆心为坐标原点，分别取OA、OB、AB的中点D、E、P，则四边形ODEF为平行四边形，易知即点P与点F重合，易证点P的轨迹是圆，从而可判断②的正误；
方程2x²-5x+2=0的两根分别为可分别

1

2

与2，从而可判断③的正误；
分别求得双曲线

x2

25

-

y2

9

=1与椭圆

x2

35

+y²=1的焦点坐标，再判断④正误即可．

解答： 解：①设A，B两个定点，若|

PA

|-|

PB

|=3，则动点P的轨迹为双曲线，错误，若|AB|=3，则动点P的轨迹为两条射线，故①错误；
②过定圆C上一定点A作圆的动弦A，B，O为原点，若

OP

=

1

2

（

OA

+

OB

），则动点P的轨迹为圆．
不妨令定圆C的圆心为坐标原点，

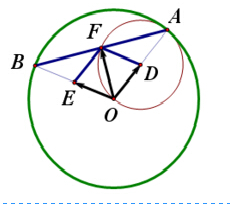
分别取OA、OB、AB的中点D、E、P，则四边形ODEF为平行四边形，

OF

=（

OD

+

OE

）=

1

2

（

OA

+

OB

），即点P与点F重合，
因为点B在圆C上，以点A为中心，将点B缩小到原来的

1

2

，得到点P，所以点P的轨迹是圆，故②错误；
③方程2x²-5x+2=0的两根分别为可分别

1

2

与2，它们可以作为椭圆和双曲线的离心率，故③正确；
④双曲线

x2

25

-

y2

9

=1的焦点坐标为（±

25+9

，0），即（±

34

，0）；椭圆

x2

35

+y²=1的焦点坐标为（±

35-1

，1），即（±

34

，0）；
它们有相同的焦点，故④正确；
综上所述，真命题的序号为③④，
故答案为：③④

点评：本题考查命题的真假判断与应用，着重考查圆锥曲线的定义性质及其应用，考查分析、运算及作图能力，属于中档题．