题目内容
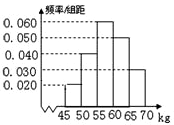 某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是
某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是考点:频率分布直方图
专题:概率与统计
分析:根据频率、频数与样本容量的关系,结合频率分布直方图中的数据,进行计算即可.
解答:
解:根据频率分布直方图,得;
被调查的学生中体重不足55kg的频率是(0.020+0.040)×5=0.300,
∴样本容量是
=120;
又∵被调查的高一新生体重在50kg至65kg的频率是(0.040+0.060+0.050)×5=0.750
∴体重在50kg至65kg的人数是120×0.75=90.
故答案为:90.
被调查的学生中体重不足55kg的频率是(0.020+0.040)×5=0.300,
∴样本容量是
| 36 |
| 0.300 |
又∵被调查的高一新生体重在50kg至65kg的频率是(0.040+0.060+0.050)×5=0.750
∴体重在50kg至65kg的人数是120×0.75=90.
故答案为:90.
点评:本题考查了频率分布直方图的应用问题,解题时利用频率=
进行解答,是基础题.
| 频数 |
| 样本容量 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,若函数g(x)=f(x)-kx有零点,则实数k的取值范围是( )
|
| A、(-∞,+∞) | ||
B、[
| ||
C、(-∞,
| ||
| D、(-∞,1) |
已知椭圆
+y2=1,则椭圆的焦距长为( )
| x2 |
| 4 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
设集合S={x|x>-2},T={x|-4≤x≤1},则(∁RS)∪T=( )
| A、(-2,1] |
| B、(-∞,-4] |
| C、(-∞,1] |
| D、[1,+∞) |
