题目内容
求函数y=sin(
x+
)+cos(
x-
)+7的最小正周期.
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:化简可得y=2sin(
+
)+7,根据三角函数的周期性及其求法可得.
| x |
| 2 |
| π |
| 3 |
解答:
解:y=sin(
x+
)+cos(
x-
)+7
=
sin
+
cos
+[
cos
+
sin
]+7
=2sin(
+
)+7
故最小正周期T=
=
=4π.
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
=
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
=2sin(
| x |
| 2 |
| π |
| 3 |
故最小正周期T=
| 2π |
| ω |
| 2π | ||
|
点评:本题主要考察了三角函数中的恒等变换应用,三角函数的周期性及其求法,属于基础题.

练习册系列答案
相关题目
已知f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)=2x-2,则不等式f(log2x)>0的解集为( )
A、(0,
| ||
B、(
| ||
| C、(2,+∞) | ||
D、(0,
|
函数f(x)=log2(-x2+ax+3)在(2,4)是单调递减的,则a的范围是( )
A、(
| ||
B、[
| ||
| C、[8,+∞) | ||
| D、(-∞,4] |
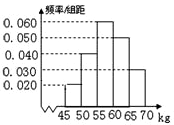 某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是
某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是