题目内容
已知函数f（x）=
，若函数g（x）=f（x）-kx有零点，则实数k的取值范围是（ ）
|
| A、（-∞，+∞） | ||
B、[
| ||
C、（-∞，
| ||
| D、（-∞，1） |
考点：函数零点的判定定理
专题：计算题,数形结合,函数的性质及应用
分析：画出f（x）的图象，函数g（x）=f（x）-kx有零点，即为y=f（x）的图象和直线y=kx有交点，作出直线y=kx，由图象观察k≤0，直线和曲线有交点，设直线y=kx与曲线y=log2x相切的切点为p（m，n），运用导数，求出切线的斜率，再由图象观察即可得到k的取值范围．
解答：
解：函数f（x）=
，
画出f（x）的图象，
函数g（x）=f（x）-kx有零点，
即为y=f（x）的图象和直线y=kx有交点，
作出直线y=kx，
由图象观察k≤0，直线和曲线有交点，
设直线y=kx与曲线y=log2x相切的切点
为p（m，n），由于（log2x）′=
，即切线的斜率为
=k，
又n=km，n=log2m，解得m=e，k=
，
则k＞0时，直线与曲线有交点，则0＜k≤
，
综上，可得实数k的取值范围是：（-∞，
]．
故选C．
解：函数f（x）=
|
画出f（x）的图象，
函数g（x）=f（x）-kx有零点，
即为y=f（x）的图象和直线y=kx有交点，
作出直线y=kx，
由图象观察k≤0，直线和曲线有交点，
设直线y=kx与曲线y=log2x相切的切点
为p（m，n），由于（log2x）′=
| 1 |
| xln2 |
| 1 |
| mln2 |
又n=km，n=log2m，解得m=e，k=
| 1 |
| eln2 |
则k＞0时，直线与曲线有交点，则0＜k≤
| 1 |
| eln2 |
综上，可得实数k的取值范围是：（-∞，
| 1 |
| eln2 |
故选C．
点评：本题考查分段函数及运用，考查分段函数的图象和运用，考查数形结合的思想方法，考查运用导数求切线的斜率，属于中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
在平行四边形ABCD中，点E为CD中点，
=
，
=
，则
等于（ ）
| AB |
| a |
| AD |
| b |
| BE |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
椭圆
+
=1的焦点是F1，F2，如果椭圆上一点P满足PF1⊥PF2，下面结论正确的是（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| A、P点有两个 |
| B、P点有四个 |
| C、P点不一定存在 |
| D、P点一定不存在 |
已知f（x）是定义在R上的偶函数，当x∈[0，+∞）时，f（x）=2x-2，则不等式f（log2x）＞0的解集为（ ）
A、（0，
| ||
B、（
| ||
| C、（2，+∞） | ||
D、（0，
|
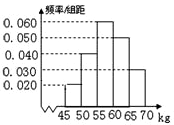某学校对高一新生的体重进行了抽样调查．如图是根据抽样调查后的数据绘制的频率分布直方图，其中体重（单位：kg）的范围是[45，70]，样本数据分组为[45，50），[50，55），[55，60），[60，65），[65，70]，已知被调查的学生中体重不足55kg的有36，则被调查的高一新生体重在50kg至65kg的人数是