题目内容
如图所示,在平行四边形ABCD中,已知AB=8,AD=5,∠DAB=60°,
=3,则
•
的值是 .

| CP |
| AP |
| BP |

考点:平面向量数量积的运算
专题:平面向量及应用
分析:由
=3
,可得
=
+
,
=
-
,进而由AB=8,AD=5,∠DAB=60°,利用向量数量积运算进而可得答案.
| CP |
| PD |
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |
解答:
解:∵
=3
,
∴
=
+
,
=
-
,
又∵AB=8,AD=5,
∴
•
=(
+
)•(
-
)=
2-
•
-
2=25-
×8×5cos60°-
×82=25-10-12=3.
故答案为3.
| CP |
| PD |
∴
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |
又∵AB=8,AD=5,
∴
| AP |
| BP |
| AD |
| 1 |
| 4 |
| AB |
| AD |
| 3 |
| 4 |
| AB |
| AD |
| 1 |
| 2 |
| AD |
| AB |
| 3 |
| 16 |
| AB |
| 1 |
| 2 |
| 3 |
| 16 |
故答案为3.
点评:本题考查的知识点是向量在几何中的应用,平面向量数量积的运算,其中根据
=3
,可得
=
+
,
=
-
,是解答的关键,属于中档题.
| CP |
| PD |
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=log2(-x2+ax+3)在(2,4)是单调递减的,则a的范围是( )
A、(
| ||
B、[
| ||
| C、[8,+∞) | ||
| D、(-∞,4] |
已知实数R为全集,集合A={x|y=log2(x-1)},B={y|y=
},则(∁RA)∩B等于( )
| 4x-x2 |
| A、(-∞,1] |
| B、(0,1) |
| C、[0,1] |
| D、(1,2] |
三个数a=0.22,b=log
2,c=20.2之间的大小关系是( )
| 1 |
| 3 |
| A、a<c<b |
| B、b<a<c |
| C、a<b<c |
| D、b<c<a |
数列{an}的各项为正数,其前n项和Sn=4-(
)n-2(n∈N*).若Tn=a1a2+a2a3+…+anan+1(n∈N*),则Tn的取值所在的区间最恰当的是( )
| 1 |
| 2 |
A、(0,
| ||
| B、[2,4) | ||
C、[2,
| ||
| D、(0,4) |
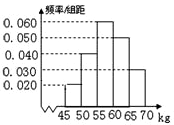 某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是
某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是