题目内容
已知集合A={x|a-1≤x≤2a+3},B={x|-2≤x≤4},全集U=R
(Ⅰ)当a=2时,求A∪B和(∁RA)∩B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
(Ⅰ)当a=2时,求A∪B和(∁RA)∩B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(Ⅰ)把a=2代入A确定出A,求出A∪B和(∁RA)∩B即可;
(Ⅱ)由A与B的交集为A,得到A为B的子集,分A为空集与A不为空集两种情况求出a的范围即可.
(Ⅱ)由A与B的交集为A,得到A为B的子集,分A为空集与A不为空集两种情况求出a的范围即可.
解答:
解:(Ⅰ)当a=2时,A={x|1<x<5},
则A∪B={x|-2<x<5},∁RA={x|x≤-1或x≥5},(∁RA)∩B={x|-2≤x<-1};
(Ⅱ)∵A∩B=A,∴A⊆B,
①若A=∅,则a-1≥2a+3,解得a≤-4;
②若A≠∅,由A⊆B,得到
,
解得:-1≤a≤
,
综上:a的取值范围是(-∞,-4]∪[-1,
].
则A∪B={x|-2<x<5},∁RA={x|x≤-1或x≥5},(∁RA)∩B={x|-2≤x<-1};
(Ⅱ)∵A∩B=A,∴A⊆B,
①若A=∅,则a-1≥2a+3,解得a≤-4;
②若A≠∅,由A⊆B,得到
|
解得:-1≤a≤
| 1 |
| 2 |
综上:a的取值范围是(-∞,-4]∪[-1,
| 1 |
| 2 |
点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
椭圆
+
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,下面结论正确的是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、P点有两个 |
| B、P点有四个 |
| C、P点不一定存在 |
| D、P点一定不存在 |
下列说法中错误的是( )
A、若f(x)=x2-3,g(x)=
| ||||||
| B、若函数的定义域只含有一个元素,则该函数的值域也只含有一个元素 | ||||||
| C、函数y=2x(x∈N)的图象是一条直线 | ||||||
D、y=
|
由函数y=ex,y=e及直线x=0所围成的图形的面积为( )
| A、1 | ||
B、
| ||
| C、e | ||
| D、2 |
已知集合A={y|y=2sin(2x-
)+1,x∈(-
,
)},集合B={x|y=lg(x2+x)},设全集U=R,则A∩(∁UB)等于( )
| π |
| 3 |
| π |
| 12 |
| π |
| 2 |
| A、[3,+∞) |
| B、(-1,0] |
| C、(3,+∞) |
| D、[-1,0] |
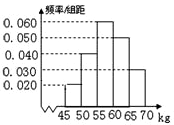 某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是
某学校对高一新生的体重进行了抽样调查.如图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是