Question

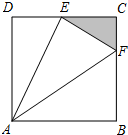如图，ABCD是边长为1百米的正方形区域，现规划建造一块景观带△ECF，其中动点E、F分别在CD、BC上，且△ECF的周长为常数a（单位：百米）．
（1）求景观带面积的最大值；
（2）当a=2时，请计算出从A点欣赏此景观带的视角（即∠EAF）．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：（1）设EC=x，CF=y，则x+y+

x2+y2

=a，利用基本不等式，结合△ECF的面积S=

1

2

xy，即可求出景观带面积的最大值；
（2）记∠EAD=α，∠FAB=β，α，β∈（0，

π

2

），α+β∈（0，

π

2

），利用和角的正切公式，即可得出结论．

解答： 解：（1）设EC=x，CF=y，则x+y+

x2+y2

=a（※）
由基本不等式，x+y+

x2+y2

≥2

xy

+

2xy

=（2+

2

）

xy

，
所以，△ECF的面积S=

1

2

xy≤

1

2

(

a

2+ 2

)2=

3-2 2

4

a2，
当且仅当x=y=

2- 2

2

a时等号成立
故景观带面积的最大值为

3-2 2

4

a2，
（2）记∠EAD=α，∠FAB=β，α，β∈（0，

π

2

），α+β∈（0，

π

2

），
则tanα=1-x，tanβ=1-y，
故tan（α+β）=

2-x-y

1-(1-x)(1-y)

=

2-(x+y)

x+y-xy

由（※）可得，xy=a（x+y）-

a2

2

，即xy=2（x+y）-2，
代入上式可得，tan（α+β）=1，
所以α+β=

π

4

，
所以∠EAF=

π

2

-（α+β）=

π

4

，
故当a=2时，视角∠EAF为定值

π

4

点评：本题考查三角函数知识的运用，考查和角公式的运用，考查面积的最值，考查学生分析解决问题的能力，属于中档题．