题目内容
已知椭圆C的中心在坐标原点O,左顶点A(-2,0),离心率e=
,F为右焦点,过焦点F的直线交椭圆C于P、Q两点(不同于点A).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△APQ的面积S=
时,求直线PQ的方程;
(Ⅲ)求
•
的范围.
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△APQ的面积S=
18
| ||
| 7 |
(Ⅲ)求
| OP |
| FP |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出a=2,e=
=
,由此能求出椭圆方程.
(Ⅱ)法一:椭圆右焦点F(1,0). 设直线PQ方程为x=my+1(m∈R).由
,得(3m2+4)y2+6my-9=0,由此利用根的判别式和韦达定理能求出直线PQ的方程.
法二:由已知条件,先求出|PQ|=12×
.再求出点A到直线PQ的距离d,由△APQ的面积S=
=
|PQ|•d,求出m,由此能求出直线PQ方程.
(Ⅲ)设P的坐标((x0,y0),由已知条件推导出
•
=
-x0+3=
(x0-2)2+2,由此能求出
•
的范围.
| c |
| a |
| 1 |
| 2 |
(Ⅱ)法一:椭圆右焦点F(1,0). 设直线PQ方程为x=my+1(m∈R).由
|
法二:由已知条件,先求出|PQ|=12×
| m2+1 |
| 3m2+4 |
18
| ||
| 7 |
| 1 |
| 2 |
(Ⅲ)设P的坐标((x0,y0),由已知条件推导出
| OP |
| FP |
| 1 |
| 4 |
| x | 2 0 |
| 1 |
| 4 |
| OP |
| FP |
解答:
解:(Ⅰ)设椭圆方程为
+
=1,(a>b>0),
∵椭圆C的中心在坐标原点O,左顶点A(-2,0),离心率e=
,
∴a=2,e=
=
∴c=1,b2=a2-c2=3,(2分)
∴椭圆方程为
+
=1.(4分)
(Ⅱ)解法一:椭圆右焦点F(1,0). 设直线PQ方程为x=my+1(m∈R).(5分)
由
,得(3m2+4)y2+6my-9=0.①(6分)
显然,方程①的△>0.设P(x1,y1),Q(x2,y2),
则有y1+y2=-
,y1y2 =-
.(8分)
由△APQ的面积S=
=
|AF|•|y1-y2|
=
,解得:m=±1.
∴直线PQ 方程为x=±y+1,
即x+y-1=0或x-y-1=0.(10分)
解法二:|PQ|=
=
=12
=12×
.(6分)
点A到直线PQ的距离d=
=
,(8分)
由△APQ的面积S=
=
|PQ|•d=•12•
•
,解得m=±1.
∴直线PQ方程为x=±y+1,即x+y-1=0或x-y-1=0.(10分)
(Ⅲ)设P的坐标((x0,y0),
则
+
=1,∴
=3-
,
∴
•
=(x0,y0)•(x0-1,y0)=x02-x0+y02
=
-x0+3=
(x0-2)2+2,(12分)
∵-2<x0<2,∴
•
的范围为(2,6).(14分)
(注:以上解答题其他解法相应给分)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的中心在坐标原点O,左顶点A(-2,0),离心率e=
| 1 |
| 2 |
∴a=2,e=
| c |
| a |
| 1 |
| 2 |
∴c=1,b2=a2-c2=3,(2分)
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)解法一:椭圆右焦点F(1,0). 设直线PQ方程为x=my+1(m∈R).(5分)
由
|
显然,方程①的△>0.设P(x1,y1),Q(x2,y2),
则有y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
由△APQ的面积S=
18
| ||
| 7 |
| 1 |
| 2 |
=
| 3 |
| 2 |
|
∴直线PQ 方程为x=±y+1,
即x+y-1=0或x-y-1=0.(10分)
解法二:|PQ|=
| (m2+1)(y1-y2)2 |
=
(m2+1)[
|
=12
|
| m2+1 |
| 3m2+4 |
点A到直线PQ的距离d=
| |-2-1| | ||
|
| 3 | ||
|
由△APQ的面积S=
18
| ||
| 7 |
| 1 |
| 2 |
| m2+1 |
| 3m2+4 |
| 3 | ||
|
∴直线PQ方程为x=±y+1,即x+y-1=0或x-y-1=0.(10分)
(Ⅲ)设P的坐标((x0,y0),
则
| ||
| 4 |
| ||
| 3 |
| y | 2 0 |
| 3 |
| 4 |
| x | 2 0 |
∴
| OP |
| FP |
=
| 1 |
| 4 |
| x | 2 0 |
| 1 |
| 4 |
∵-2<x0<2,∴
| OP |
| FP |
(注:以上解答题其他解法相应给分)
点评:本题考查椭圆方程的求法,考查直线方程的求法,考查向量的数量积的取值范围的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
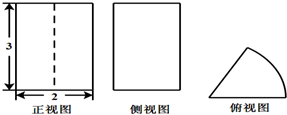 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
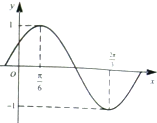 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<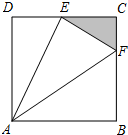 如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米).
如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米).