题目内容
3.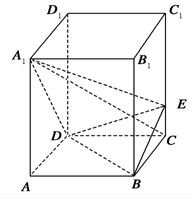 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.(1)求证:A1C⊥平面BED;
(2)求三棱锥A1-BED的体积.
分析 (1)法一(几何法):连结AC交BD于点F,则BD⊥AC,BD⊥A1C.在平面A1CA内,连结EF交A1C于点G,推导出A1C⊥EF.由此能证明A1C⊥平面BED.
法二(向量法):以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明A1C⊥平面BED.
(2)求出cos<$\overrightarrow{DE},\overrightarrow{DB}$>,从而得到sin<$\overrightarrow{DE}$,$\overrightarrow{DB}$>,进而求出S△DBE,再由A1C⊥平面BED,能求出三棱锥A1-BED的体积.
解答 证明:(1)证法一(几何法):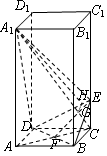
依题设知AB=2,CE=1.
连结AC交BD于点F,则BD⊥AC.
由三垂线定理知,BD⊥A1C.在平面A1CA内,连结EF交A1C于点G,
由于$\frac{{A}_{1}A}{FC}$=$\frac{AC}{CE}$=2$\sqrt{2}$,
故Rt△A1AC∽Rt△FCE,∠AA1C=∠CFE,
∠CFE与∠FCA1互余.于是A1C⊥EF.
A1C与平面BED内两条相交直线BD,EF都垂直,
∴A1C⊥平面BED.
证法二(向量法):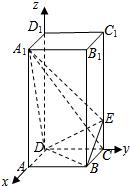 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(2,0,4),C(0,2,0),B(2,2,0),D(0,0,0),E(0,2,1),
∴$\overrightarrow{{A}_{1}C}$=(-2,2,-4),$\overrightarrow{DE}$=(0,2,1),$\overrightarrow{DB}$=(2,2,0),
∵$\overrightarrow{{A}_{1}C}$•$\overrightarrow{DE}$=0+4-4=0,$\overrightarrow{{A}_{1}C}$•$\overrightarrow{DB}$=-4+4+0=0,
∴A1C⊥DE,A1C⊥DB,
又DE∩DB=D,∴A1C⊥平面BED.
解:(2)cos<$\overrightarrow{DE},\overrightarrow{DB}$>=$\frac{|\overrightarrow{DE},\overrightarrow{DB}|}{|\overrightarrow{DE}|•|\overrightarrow{DB}|}$=$\frac{4}{\sqrt{5}•\sqrt{8}}$=$\frac{\sqrt{10}}{5}$,
∴sin<$\overrightarrow{DE}$,$\overrightarrow{DB}$>=$\sqrt{1-\frac{10}{25}}$=$\frac{\sqrt{15}}{5}$,
|$\overrightarrow{DE}$|=$\sqrt{5}$,|$\overrightarrow{DB}$|=2$\sqrt{2}$,|$\overrightarrow{{A}_{1}C}$|=$\sqrt{4+4+16}$=2$\sqrt{6}$,
∴${S}_{△DBE}=\frac{1}{2}×\sqrt{5}×2\sqrt{6}×\frac{\sqrt{15}}{5}$=3$\sqrt{2}$,
∵A1C⊥平面BED,
∴三棱锥A1-BED的体积V=$\frac{1}{3}×|{A}_{1}C|×{S}_{△DBE}$=$\frac{1}{3}×2\sqrt{6}×3\sqrt{2}$=4$\sqrt{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| x | 8 | 12 | 13 | a | 18 |
| y | 10 | 8 | 6 | 7 | 4 |
| A. | (0,2) | B. | (1,0) | C. | (2,0) | D. | (0,1) |
| A. | 取出的鞋不成对的概率是$\frac{4}{5}$ | |
| B. | 取出的鞋都是左脚的概率是$\frac{1}{5}$ | |
| C. | 取出的鞋都是同一只脚的概率是$\frac{2}{5}$ | |
| D. | 取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是$\frac{12}{25}$ |