题目内容
18.在△ABC中,已知$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\overrightarrow{BC}$•$\overrightarrow{CA}$,则△ABC为等腰三角形.分析 运用向量的运算和向量的平方即为向量模的平方,结合平方差公式,即可判断三角形的形状.
解答 解:在△ABC中,$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\overrightarrow{BC}$•$\overrightarrow{CA}$,
可得$\overrightarrow{AB}$•$\overrightarrow{BC}$-$\overrightarrow{BC}$•$\overrightarrow{CA}$=0,
即为$\overrightarrow{BC}$•($\overrightarrow{AB}$-$\overrightarrow{CA}$)=0,
即有($\overrightarrow{AC}$-$\overrightarrow{AB}$)•($\overrightarrow{AC}$+$\overrightarrow{AB}$)=0,
即有$\overrightarrow{AC}$2=$\overrightarrow{AB}$2,
即为|$\overrightarrow{AC}$||2=|$\overrightarrow{AB}$|2,
可得|$\overrightarrow{AC}$||=|$\overrightarrow{AB}$|,
可得三角形ABC为等腰三角形.
故答案为:等腰.
点评 本题考查向量的运算和三角形的形状的判断,注意运用向量模的平方即为向量的平方,考查化简整理能力,属于基础题.

练习册系列答案
相关题目
6.一个物体的运动方程为s=t2-t+2(其中s的单位是米,t的单位是秒),那么物体在t=4秒的瞬时速度是( )
| A. | 6米/秒 | B. | 7米/秒 | C. | 8米/秒 | D. | 9米/秒 |
13.平面向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x=( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
3.已知sin(30°+α)=$\frac{3}{5}$,60°<α<150°,则cosα的值是( )
| A. | $\frac{3\sqrt{3}-4}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
10.双曲线$\frac{{x}^{2}}{4}$-y2=1的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
4.直线x=-$\frac{p}{2}$和圆x2+y2+6x+8=0相切,则实数p=( )
| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |
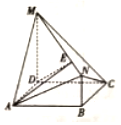 如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.
如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.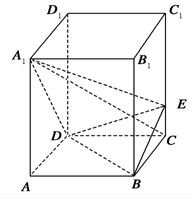 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.